fitrtree
Fit binary decision tree for regression
Syntax
Description
tree = fitrtree(Tbl,ResponseVarName)Tbl and the
output (response) contained in Tbl.ResponseVarName. The
returned tree is a binary tree where each branching node is
split based on the values of a column of Tbl.
tree = fitrtree(___,Name,Value)
Examples
Construct Regression Tree
Load the sample data.
load carsmallConstruct a regression tree using the sample data. The response variable is miles per gallon, MPG.
tree = fitrtree([Weight, Cylinders],MPG,... 'CategoricalPredictors',2,'MinParentSize',20,... 'PredictorNames',{'W','C'})
tree =
RegressionTree
PredictorNames: {'W' 'C'}
ResponseName: 'Y'
CategoricalPredictors: 2
ResponseTransform: 'none'
NumObservations: 94
Predict the mileage of 4,000-pound cars with 4, 6, and 8 cylinders.
MPG4Kpred = predict(tree,[4000 4; 4000 6; 4000 8])
MPG4Kpred = 3×1
19.2778
19.2778
14.3889
Control Regression Tree Depth
fitrtree grows deep decision trees by default. You can grow shallower trees to reduce model complexity or computation time. To control the depth of trees, use the 'MaxNumSplits', 'MinLeafSize', or 'MinParentSize' name-value pair arguments.
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];The default values of the tree-depth controllers for growing regression trees are:
n - 1forMaxNumSplits.nis the training sample size.1forMinLeafSize.10forMinParentSize.
These default values tend to grow deep trees for large training sample sizes.
Train a regression tree using the default values for tree-depth control. Cross-validate the model using 10-fold cross-validation.
rng(1); % For reproducibility MdlDefault = fitrtree(X,MPG,'CrossVal','on');
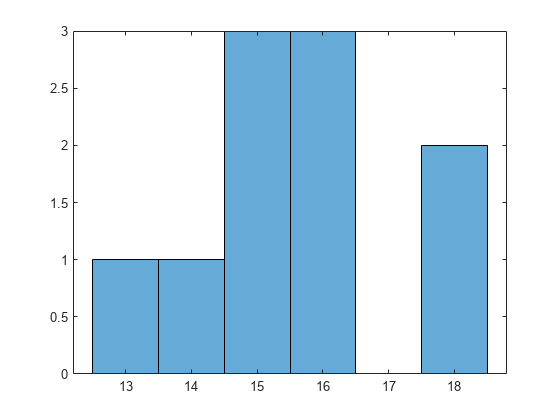
Draw a histogram of the number of imposed splits on the trees. The number of imposed splits is one less than the number of leaves. Also, view one of the trees.
numBranches = @(x)sum(x.IsBranch); mdlDefaultNumSplits = cellfun(numBranches, MdlDefault.Trained); figure; histogram(mdlDefaultNumSplits)
view(MdlDefault.Trained{1},'Mode','graph')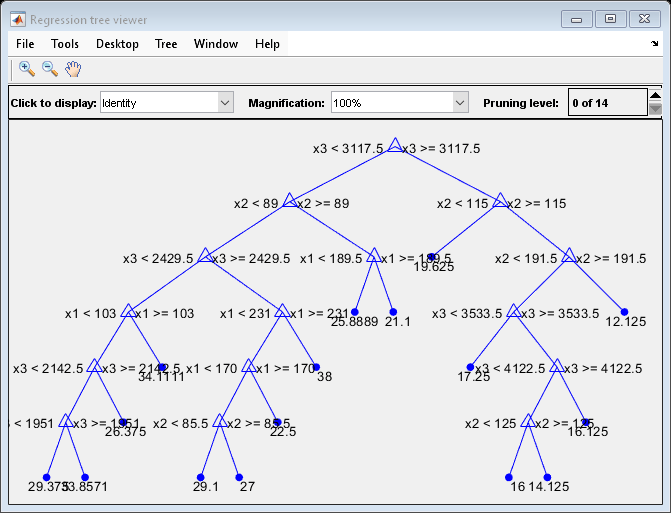
The average number of splits is between 14 and 15.
Suppose that you want a regression tree that is not as complex (deep) as the ones trained using the default number of splits. Train another regression tree, but set the maximum number of splits at 7, which is about half the mean number of splits from the default regression tree. Cross-validate the model using 10-fold cross-validation.
Mdl7 = fitrtree(X,MPG,'MaxNumSplits',7,'CrossVal','on'); view(Mdl7.Trained{1},'Mode','graph')
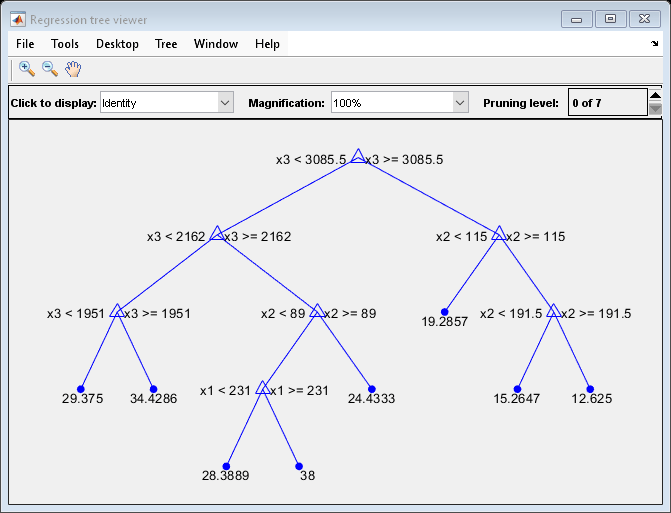
Compare the cross-validation mean squared errors (MSEs) of the models.
mseDefault = kfoldLoss(MdlDefault)
mseDefault = 25.7383
mse7 = kfoldLoss(Mdl7)
mse7 = 26.5748
Mdl7 is much less complex and performs only slightly worse than MdlDefault.
Optimize Regression Tree
Optimize hyperparameters automatically using fitrtree.
Load the carsmall data set.
load carsmallUse Weight and Horsepower as predictors for MPG. Find hyperparameters that minimize five-fold cross-validation loss by using automatic hyperparameter optimization.
For reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function.
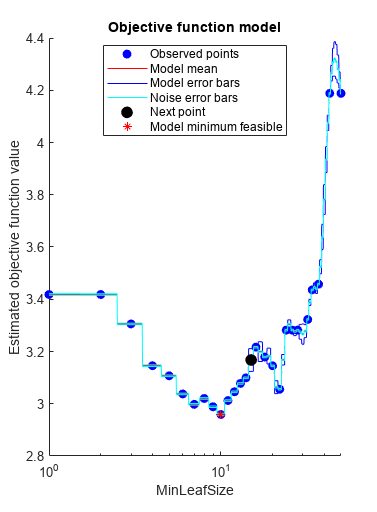
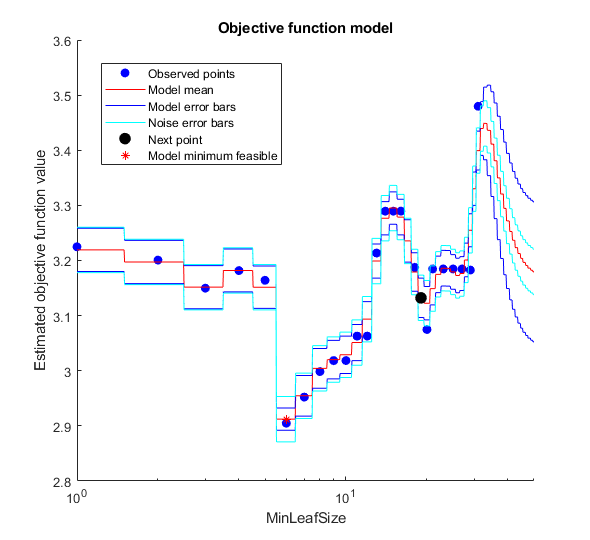
X = [Weight,Horsepower]; Y = MPG; rng default Mdl = fitrtree(X,Y,'OptimizeHyperparameters','auto',... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName',... 'expected-improvement-plus'))
|======================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | MinLeafSize |
| | result | log(1+loss) | runtime | (observed) | (estim.) | |
|======================================================================================|
| 1 | Best | 3.2818 | 0.17856 | 3.2818 | 3.2818 | 28 |
| 2 | Accept | 3.4183 | 0.10154 | 3.2818 | 3.2888 | 1 |
| 3 | Best | 3.1457 | 0.05041 | 3.1457 | 3.1628 | 4 |
| 4 | Best | 2.9885 | 0.060213 | 2.9885 | 2.9885 | 9 |
| 5 | Accept | 2.9978 | 0.081682 | 2.9885 | 2.9885 | 7 |
| 6 | Accept | 3.0203 | 0.045349 | 2.9885 | 3.0013 | 8 |
| 7 | Accept | 2.9885 | 0.071842 | 2.9885 | 2.9981 | 9 |
| 8 | Best | 2.9589 | 0.05939 | 2.9589 | 2.9589 | 10 |
| 9 | Accept | 3.078 | 0.036471 | 2.9589 | 2.9888 | 13 |
| 10 | Accept | 4.1881 | 0.045413 | 2.9589 | 2.9592 | 50 |
| 11 | Accept | 3.4182 | 0.084952 | 2.9589 | 2.9592 | 2 |
| 12 | Accept | 3.0376 | 0.038532 | 2.9589 | 2.9591 | 6 |
| 13 | Accept | 3.1453 | 0.039329 | 2.9589 | 2.9591 | 20 |
| 14 | Accept | 2.9589 | 0.048311 | 2.9589 | 2.959 | 10 |
| 15 | Accept | 3.0123 | 0.035575 | 2.9589 | 2.9728 | 11 |
| 16 | Accept | 2.9589 | 0.039667 | 2.9589 | 2.9593 | 10 |
| 17 | Accept | 3.3055 | 0.048941 | 2.9589 | 2.9593 | 3 |
| 18 | Accept | 2.9589 | 0.082784 | 2.9589 | 2.9592 | 10 |
| 19 | Accept | 3.4577 | 0.0753 | 2.9589 | 2.9591 | 37 |
| 20 | Accept | 3.2166 | 0.035505 | 2.9589 | 2.959 | 16 |
|======================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | MinLeafSize |
| | result | log(1+loss) | runtime | (observed) | (estim.) | |
|======================================================================================|
| 21 | Accept | 3.107 | 0.043718 | 2.9589 | 2.9591 | 5 |
| 22 | Accept | 3.2818 | 0.038819 | 2.9589 | 2.959 | 24 |
| 23 | Accept | 3.3226 | 0.029256 | 2.9589 | 2.959 | 32 |
| 24 | Accept | 4.1881 | 0.10829 | 2.9589 | 2.9589 | 43 |
| 25 | Accept | 3.1789 | 0.031267 | 2.9589 | 2.9589 | 18 |
| 26 | Accept | 3.0992 | 0.043228 | 2.9589 | 2.9589 | 14 |
| 27 | Accept | 3.0556 | 0.045482 | 2.9589 | 2.9589 | 22 |
| 28 | Accept | 3.0459 | 0.038532 | 2.9589 | 2.9589 | 12 |
| 29 | Accept | 3.2818 | 0.078529 | 2.9589 | 2.9589 | 26 |
| 30 | Accept | 3.4361 | 0.035617 | 2.9589 | 2.9589 | 34 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 21.1606 seconds
Total objective function evaluation time: 1.7525
Best observed feasible point:
MinLeafSize
___________
10
Observed objective function value = 2.9589
Estimated objective function value = 2.9589
Function evaluation time = 0.05939
Best estimated feasible point (according to models):
MinLeafSize
___________
10
Estimated objective function value = 2.9589
Estimated function evaluation time = 0.052838

Mdl =
RegressionTree
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
Unbiased Predictor Importance Estimates
Load the carsmall data set. Consider a model that predicts the mean fuel economy of a car given its acceleration, number of cylinders, engine displacement, horsepower, manufacturer, model year, and weight. Consider Cylinders, Mfg, and Model_Year as categorical variables.
load carsmall Cylinders = categorical(Cylinders); Mfg = categorical(cellstr(Mfg)); Model_Year = categorical(Model_Year); X = table(Acceleration,Cylinders,Displacement,Horsepower,Mfg, ... Model_Year,Weight,MPG);
Display the number of categories represented in the categorical variables.
numCylinders = numel(categories(Cylinders))
numCylinders = 3
numMfg = numel(categories(Mfg))
numMfg = 28
numModelYear = numel(categories(Model_Year))
numModelYear = 3
Because there are 3 categories only in Cylinders and Model_Year, the standard CART, predictor-splitting algorithm prefers splitting a continuous predictor over these two variables.
Train a regression tree using the entire data set. To grow unbiased trees, specify usage of the curvature test for splitting predictors. Because there are missing values in the data, specify usage of surrogate splits.
Mdl = fitrtree(X,"MPG",PredictorSelection="curvature",Surrogate="on");
Estimate predictor importance values by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. Compare the estimates using a bar graph.
imp = predictorImportance(Mdl); figure bar(imp) title("Predictor Importance Estimates") ylabel("Estimates") xlabel("Predictors") h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = "none";
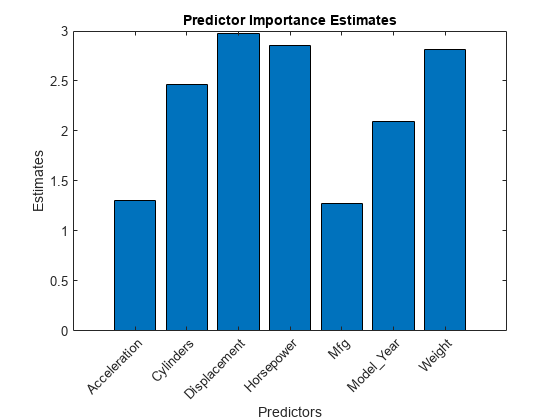
In this case, Displacement is the most important predictor, followed by Horsepower.
Control Maximum Tree Depth on Tall Array
fitrtree grows deep decision trees by default. Build a shallower tree that requires fewer passes through a tall array. Use the 'MaxDepth' name-value pair argument to control the maximum tree depth.
When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. If you want to run the example using the local MATLAB session when you have Parallel Computing Toolbox, you can change the global execution environment by using the mapreducer function.
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];Convert the in-memory arrays X and MPG to tall arrays.
tx = tall(X);
Starting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
ty = tall(MPG);
Grow a regression tree using all observations. Allow the tree to grow to the maximum possible depth.
For reproducibility, set the seeds of the random number generators using rng and tallrng. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.
rng('default') tallrng('default') Mdl = fitrtree(tx,ty);
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 2: Completed in 4.1 sec - Pass 2 of 2: Completed in 0.71 sec Evaluation completed in 6.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 1.4 sec - Pass 2 of 7: Completed in 0.29 sec - Pass 3 of 7: Completed in 1.5 sec - Pass 4 of 7: Completed in 3.3 sec - Pass 5 of 7: Completed in 0.63 sec - Pass 6 of 7: Completed in 1.2 sec - Pass 7 of 7: Completed in 2.6 sec Evaluation completed in 12 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.36 sec - Pass 2 of 7: Completed in 0.27 sec - Pass 3 of 7: Completed in 0.85 sec - Pass 4 of 7: Completed in 2 sec - Pass 5 of 7: Completed in 0.55 sec - Pass 6 of 7: Completed in 0.92 sec - Pass 7 of 7: Completed in 1.6 sec Evaluation completed in 7.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.32 sec - Pass 2 of 7: Completed in 0.29 sec - Pass 3 of 7: Completed in 0.89 sec - Pass 4 of 7: Completed in 1.9 sec - Pass 5 of 7: Completed in 0.83 sec - Pass 6 of 7: Completed in 1.2 sec - Pass 7 of 7: Completed in 2.4 sec Evaluation completed in 9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.33 sec - Pass 2 of 7: Completed in 0.28 sec - Pass 3 of 7: Completed in 0.89 sec - Pass 4 of 7: Completed in 2.4 sec - Pass 5 of 7: Completed in 0.76 sec - Pass 6 of 7: Completed in 1 sec - Pass 7 of 7: Completed in 1.7 sec Evaluation completed in 8.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.34 sec - Pass 2 of 7: Completed in 0.26 sec - Pass 3 of 7: Completed in 0.81 sec - Pass 4 of 7: Completed in 1.7 sec - Pass 5 of 7: Completed in 0.56 sec - Pass 6 of 7: Completed in 1 sec - Pass 7 of 7: Completed in 1.9 sec Evaluation completed in 7.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.35 sec - Pass 2 of 7: Completed in 0.28 sec - Pass 3 of 7: Completed in 0.81 sec - Pass 4 of 7: Completed in 1.8 sec - Pass 5 of 7: Completed in 0.76 sec - Pass 6 of 7: Completed in 0.96 sec - Pass 7 of 7: Completed in 2.2 sec Evaluation completed in 8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.35 sec - Pass 2 of 7: Completed in 0.32 sec - Pass 3 of 7: Completed in 0.92 sec - Pass 4 of 7: Completed in 1.9 sec - Pass 5 of 7: Completed in 1 sec - Pass 6 of 7: Completed in 1.5 sec - Pass 7 of 7: Completed in 2.1 sec Evaluation completed in 9.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.33 sec - Pass 2 of 7: Completed in 0.28 sec - Pass 3 of 7: Completed in 0.82 sec - Pass 4 of 7: Completed in 1.4 sec - Pass 5 of 7: Completed in 0.61 sec - Pass 6 of 7: Completed in 0.93 sec - Pass 7 of 7: Completed in 1.5 sec Evaluation completed in 6.6 sec
View the trained tree Mdl.
view(Mdl,'Mode','graph')
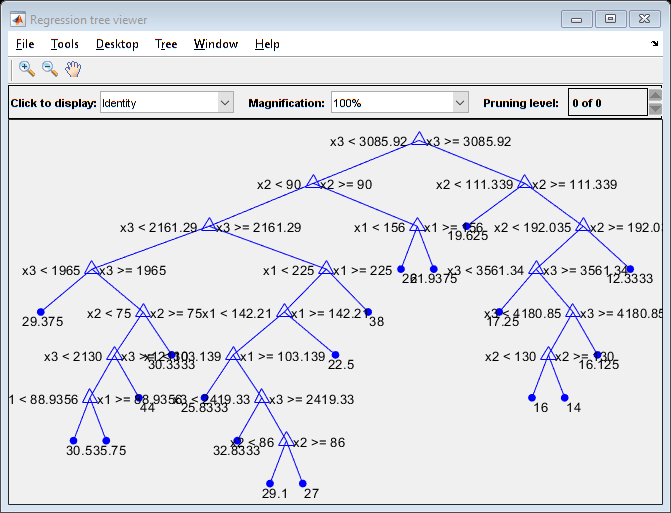
Mdl is a tree of depth 8.
Estimate the in-sample mean squared error.
MSE_Mdl = gather(loss(Mdl,tx,ty))
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.6 sec Evaluation completed in 1.9 sec
MSE_Mdl = 4.9078
Grow a regression tree using all observations. Limit the tree depth by specifying a maximum tree depth of 4.
Mdl2 = fitrtree(tx,ty,'MaxDepth',4);Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 2: Completed in 0.27 sec - Pass 2 of 2: Completed in 0.28 sec Evaluation completed in 0.84 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.36 sec - Pass 2 of 7: Completed in 0.3 sec - Pass 3 of 7: Completed in 0.95 sec - Pass 4 of 7: Completed in 1.6 sec - Pass 5 of 7: Completed in 0.55 sec - Pass 6 of 7: Completed in 0.93 sec - Pass 7 of 7: Completed in 1.5 sec Evaluation completed in 7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.34 sec - Pass 2 of 7: Completed in 0.3 sec - Pass 3 of 7: Completed in 0.95 sec - Pass 4 of 7: Completed in 1.7 sec - Pass 5 of 7: Completed in 0.57 sec - Pass 6 of 7: Completed in 0.94 sec - Pass 7 of 7: Completed in 1.8 sec Evaluation completed in 7.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.34 sec - Pass 2 of 7: Completed in 0.3 sec - Pass 3 of 7: Completed in 0.87 sec - Pass 4 of 7: Completed in 1.5 sec - Pass 5 of 7: Completed in 0.57 sec - Pass 6 of 7: Completed in 0.81 sec - Pass 7 of 7: Completed in 1.7 sec Evaluation completed in 6.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 7: Completed in 0.32 sec - Pass 2 of 7: Completed in 0.27 sec - Pass 3 of 7: Completed in 0.85 sec - Pass 4 of 7: Completed in 1.6 sec - Pass 5 of 7: Completed in 0.63 sec - Pass 6 of 7: Completed in 0.9 sec - Pass 7 of 7: Completed in 1.6 sec Evaluation completed in 7 sec
View the trained tree Mdl2.
view(Mdl2,'Mode','graph')
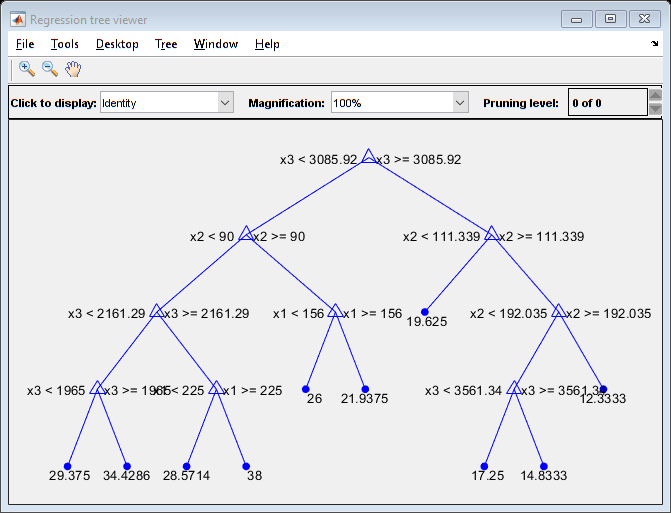
Estimate the in-sample mean squared error.
MSE_Mdl2 = gather(loss(Mdl2,tx,ty))
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.73 sec Evaluation completed in 1 sec
MSE_Mdl2 = 9.3903
Mdl2 is a less complex tree with a depth of 4 and an in-sample mean squared error that is higher than the mean squared error of Mdl.
Optimize Regression Tree on Tall Array
Optimize hyperparameters of a regression tree automatically using a tall array. The sample data set is the carsmall data set. This example converts the data set to a tall array and uses it to run the optimization procedure.
When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. If you want to run the example using the local MATLAB session when you have Parallel Computing Toolbox, you can change the global execution environment by using the mapreducer function.
Load the carsmall data set. Consider Displacement, Horsepower, and Weight as predictors of the response MPG.
load carsmall
X = [Displacement Horsepower Weight];Convert the in-memory arrays X and MPG to tall arrays.
tx = tall(X);
Starting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
ty = tall(MPG);
Optimize hyperparameters automatically using the 'OptimizeHyperparameters' name-value pair argument. Find the optimal 'MinLeafSize' value that minimizes holdout cross-validation loss. (Specifying 'auto' uses 'MinLeafSize'.) For reproducibility, use the 'expected-improvement-plus' acquisition function and set the seeds of the random number generators using rng and tallrng. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.
rng('default') tallrng('default') [Mdl,FitInfo,HyperparameterOptimizationResults] = fitrtree(tx,ty,... 'OptimizeHyperparameters','auto',... 'HyperparameterOptimizationOptions',struct('Holdout',0.3,... 'AcquisitionFunctionName','expected-improvement-plus'))
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 4.4 sec Evaluation completed in 6.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.97 sec - Pass 2 of 4: Completed in 1.6 sec - Pass 3 of 4: Completed in 3.6 sec - Pass 4 of 4: Completed in 2.4 sec Evaluation completed in 9.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 2.7 sec - Pass 4 of 4: Completed in 1.9 sec Evaluation completed in 7.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 3 sec - Pass 4 of 4: Completed in 2 sec Evaluation completed in 8.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 2.6 sec - Pass 4 of 4: Completed in 2 sec Evaluation completed in 7.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2.1 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 6.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2.4 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 6.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.4 sec Evaluation completed in 1.7 sec |======================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | MinLeafSize | | | result | log(1+loss) | runtime | (observed) | (estim.) | | |======================================================================================| | 1 | Best | 3.2007 | 69.013 | 3.2007 | 3.2007 | 2 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.52 sec Evaluation completed in 0.83 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 3 sec - Pass 4 of 4: Completed in 2 sec Evaluation completed in 8.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.79 sec Evaluation completed in 1 sec | 2 | Error | NaN | 13.772 | NaN | 3.2007 | 46 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.52 sec Evaluation completed in 0.81 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.57 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 2.2 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 6.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2.7 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 6.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2.1 sec - Pass 4 of 4: Completed in 1.9 sec Evaluation completed in 6.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.72 sec Evaluation completed in 0.99 sec | 3 | Best | 3.1876 | 29.091 | 3.1876 | 3.1884 | 18 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.48 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.64 sec Evaluation completed in 0.92 sec | 4 | Best | 2.9048 | 33.465 | 2.9048 | 2.9537 | 6 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.71 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.66 sec Evaluation completed in 0.92 sec | 5 | Accept | 3.2895 | 25.902 | 2.9048 | 2.9048 | 15 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.54 sec Evaluation completed in 0.82 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2.1 sec - Pass 4 of 4: Completed in 1.9 sec Evaluation completed in 6.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 2 sec Evaluation completed in 6.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.68 sec Evaluation completed in 0.99 sec | 6 | Accept | 3.1641 | 35.522 | 2.9048 | 3.1493 | 5 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.51 sec Evaluation completed in 0.79 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.67 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 6.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.63 sec Evaluation completed in 0.89 sec | 7 | Accept | 2.9048 | 33.755 | 2.9048 | 2.9048 | 6 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.45 sec Evaluation completed in 0.75 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2.2 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 6.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.68 sec Evaluation completed in 0.97 sec | 8 | Accept | 2.9522 | 33.362 | 2.9048 | 2.9048 | 7 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.42 sec Evaluation completed in 0.71 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.64 sec Evaluation completed in 0.9 sec | 9 | Accept | 2.9985 | 32.674 | 2.9048 | 2.9048 | 8 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.43 sec Evaluation completed in 0.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 5.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.88 sec Evaluation completed in 1.2 sec | 10 | Accept | 3.0185 | 33.922 | 2.9048 | 2.9048 | 10 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.74 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 6.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.73 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 6.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.63 sec Evaluation completed in 0.88 sec | 11 | Accept | 3.2895 | 26.625 | 2.9048 | 2.9048 | 14 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.48 sec Evaluation completed in 0.78 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.65 sec Evaluation completed in 0.9 sec | 12 | Accept | 3.4798 | 18.111 | 2.9048 | 2.9049 | 31 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.71 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.64 sec Evaluation completed in 0.91 sec | 13 | Accept | 3.2248 | 47.436 | 2.9048 | 2.9048 | 1 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.46 sec Evaluation completed in 0.74 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.57 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2.6 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 6.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.62 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 6.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.61 sec Evaluation completed in 0.88 sec | 14 | Accept | 3.1498 | 42.062 | 2.9048 | 2.9048 | 3 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.46 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.67 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 2.3 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 7.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.6 sec Evaluation completed in 0.86 sec | 15 | Accept | 2.9048 | 34.3 | 2.9048 | 2.9048 | 6 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.48 sec Evaluation completed in 0.78 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 2 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.88 sec | 16 | Accept | 2.9048 | 32.97 | 2.9048 | 2.9048 | 6 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.43 sec Evaluation completed in 0.73 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.9 sec | 17 | Accept | 3.1847 | 17.47 | 2.9048 | 2.9048 | 23 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.43 sec Evaluation completed in 0.72 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.68 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 6.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.93 sec | 18 | Accept | 3.1817 | 33.346 | 2.9048 | 2.9048 | 4 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.43 sec Evaluation completed in 0.72 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.86 sec | 19 | Error | NaN | 10.235 | 2.9048 | 2.9048 | 38 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.47 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.63 sec Evaluation completed in 0.89 sec | 20 | Accept | 3.0628 | 32.459 | 2.9048 | 2.9048 | 12 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.46 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.68 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 2.1 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 6.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.64 sec Evaluation completed in 0.9 sec |======================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | MinLeafSize | | | result | log(1+loss) | runtime | (observed) | (estim.) | | |======================================================================================| | 21 | Accept | 3.1847 | 19.02 | 2.9048 | 2.9048 | 27 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.45 sec Evaluation completed in 0.75 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.6 sec - Pass 3 of 4: Completed in 2.4 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 6.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.63 sec Evaluation completed in 0.89 sec | 22 | Accept | 3.0185 | 33.933 | 2.9048 | 2.9048 | 9 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.46 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.64 sec Evaluation completed in 0.89 sec | 23 | Accept | 3.0749 | 25.147 | 2.9048 | 2.9048 | 20 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.73 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.42 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 1.9 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.88 sec | 24 | Accept | 3.0628 | 32.764 | 2.9048 | 2.9048 | 11 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.73 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.61 sec Evaluation completed in 0.87 sec | 25 | Error | NaN | 10.294 | 2.9048 | 2.9048 | 34 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.73 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.87 sec | 26 | Accept | 3.1847 | 17.587 | 2.9048 | 2.9048 | 25 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.45 sec Evaluation completed in 0.73 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.66 sec Evaluation completed in 0.96 sec | 27 | Accept | 3.2895 | 24.867 | 2.9048 | 2.9048 | 16 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.44 sec Evaluation completed in 0.74 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.6 sec Evaluation completed in 0.88 sec | 28 | Accept | 3.2135 | 24.928 | 2.9048 | 2.9048 | 13 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.47 sec Evaluation completed in 0.76 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.45 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.46 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.62 sec Evaluation completed in 0.87 sec | 29 | Accept | 3.1847 | 17.582 | 2.9048 | 2.9048 | 21 |
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.53 sec Evaluation completed in 0.81 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.44 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.43 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 1.8 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.63 sec Evaluation completed in 0.88 sec | 30 | Accept | 3.1827 | 17.597 | 2.9048 | 2.9122 | 29 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 882.5668 seconds.
Total objective function evaluation time: 859.2122
Best observed feasible point:
MinLeafSize
___________
6
Observed objective function value = 2.9048
Estimated objective function value = 2.9122
Function evaluation time = 33.4655
Best estimated feasible point (according to models):
MinLeafSize
___________
6
Estimated objective function value = 2.9122
Estimated function evaluation time = 33.6594
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 2: Completed in 0.26 sec
- Pass 2 of 2: Completed in 0.26 sec
Evaluation completed in 0.84 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 7: Completed in 0.31 sec
- Pass 2 of 7: Completed in 0.25 sec
- Pass 3 of 7: Completed in 0.75 sec
- Pass 4 of 7: Completed in 1.2 sec
- Pass 5 of 7: Completed in 0.45 sec
- Pass 6 of 7: Completed in 0.69 sec
- Pass 7 of 7: Completed in 1.2 sec
Evaluation completed in 5.7 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 7: Completed in 0.28 sec
- Pass 2 of 7: Completed in 0.24 sec
- Pass 3 of 7: Completed in 0.75 sec
- Pass 4 of 7: Completed in 1.2 sec
- Pass 5 of 7: Completed in 0.46 sec
- Pass 6 of 7: Completed in 0.67 sec
- Pass 7 of 7: Completed in 1.2 sec
Evaluation completed in 5.6 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 7: Completed in 0.32 sec
- Pass 2 of 7: Completed in 0.25 sec
- Pass 3 of 7: Completed in 0.71 sec
- Pass 4 of 7: Completed in 1.2 sec
- Pass 5 of 7: Completed in 0.47 sec
- Pass 6 of 7: Completed in 0.66 sec
- Pass 7 of 7: Completed in 1.2 sec
Evaluation completed in 5.6 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 7: Completed in 0.29 sec
- Pass 2 of 7: Completed in 0.25 sec
- Pass 3 of 7: Completed in 0.73 sec
- Pass 4 of 7: Completed in 1.2 sec
- Pass 5 of 7: Completed in 0.46 sec
- Pass 6 of 7: Completed in 0.68 sec
- Pass 7 of 7: Completed in 1.2 sec
Evaluation completed in 5.5 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 7: Completed in 0.27 sec
- Pass 2 of 7: Completed in 0.25 sec
- Pass 3 of 7: Completed in 0.75 sec
- Pass 4 of 7: Completed in 1.2 sec
- Pass 5 of 7: Completed in 0.47 sec
- Pass 6 of 7: Completed in 0.69 sec
- Pass 7 of 7: Completed in 1.2 sec
Evaluation completed in 5.6 sec
Mdl =
CompactRegressionTree
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
Properties, Methods
FitInfo = struct with no fields.
HyperparameterOptimizationResults =
BayesianOptimization with properties:
ObjectiveFcn: @createObjFcn/tallObjFcn
VariableDescriptions: [3×1 optimizableVariable]
Options: [1×1 struct]
MinObjective: 2.9048
XAtMinObjective: [1×1 table]
MinEstimatedObjective: 2.9122
XAtMinEstimatedObjective: [1×1 table]
NumObjectiveEvaluations: 30
TotalElapsedTime: 882.5668
NextPoint: [1×1 table]
XTrace: [30×1 table]
ObjectiveTrace: [30×1 double]
ConstraintsTrace: []
UserDataTrace: {30×1 cell}
ObjectiveEvaluationTimeTrace: [30×1 double]
IterationTimeTrace: [30×1 double]
ErrorTrace: [30×1 double]
FeasibilityTrace: [30×1 logical]
FeasibilityProbabilityTrace: [30×1 double]
IndexOfMinimumTrace: [30×1 double]
ObjectiveMinimumTrace: [30×1 double]
EstimatedObjectiveMinimumTrace: [30×1 double]
Input Arguments
Tbl — Sample data
table
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
ResponseVarName — Response variable name
name of variable in Tbl
Response variable name, specified as the name of a variable in
Tbl. The response variable must be a numeric vector.
You must specify ResponseVarName as a character vector or string
scalar. For example, if Tbl stores the response variable
Y as Tbl.Y, then specify it as
'Y'. Otherwise, the software treats all columns of
Tbl, including Y, as predictors when
training the model.
Data Types: char | string
formula — Explanatory model of response variable and subset of predictor variables
character vector | string scalar
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Y — Response data
numeric column vector
Response data, specified as a numeric column vector with the
same number of rows as X. Each entry in Y is
the response to the data in the corresponding row of X.
The software considers NaN values in Y to
be missing values. fitrtree does not use observations
with missing values for Y in the fit.
Data Types: single | double
X — Predictor data
numeric matrix
Predictor data, specified as a numeric matrix. Each column of X represents
one variable, and each row represents one observation.
fitrtree considers NaN values in X
as missing values. fitrtree does not use observations with all
missing values for X in the fit. fitrtree uses
observations with some missing values for X to find splits on
variables for which these observations have valid values.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'CrossVal','on','MinParentSize',30 specifies a
cross-validated regression tree with a minimum of 30 observations per branch
node.
Note
You cannot use any cross-validation name-value argument together with the
'OptimizeHyperparameters' name-value argument. You can modify the
cross-validation for 'OptimizeHyperparameters' only by using the
'HyperparameterOptimizationOptions' name-value argument.
CategoricalPredictors — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | 'all'
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the predictor data is a table
(Tbl), fitrtree assumes that a variable is
categorical if it is a logical vector, unordered categorical vector, character array, string
array, or cell array of character vectors. If the predictor data is a matrix
(X), fitrtree assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
Example: 'CategoricalPredictors','all'
Data Types: single | double | logical | char | string | cell
MaxDepth — Maximum tree depth
positive integer
Maximum tree depth, specified as the comma-separated pair consisting
of 'MaxDepth' and a positive integer. Specify a value
for this argument to return a tree that has fewer levels and requires
fewer passes through the tall array to compute. Generally, the algorithm
of fitrtree takes one pass through the data and an
additional pass for each tree level. The function does not set a maximum
tree depth, by default.
Note
This option applies only when you use
fitrtree on tall arrays. See Tall Arrays for more information.
MergeLeaves — Leaf merge flag
'on' (default) | 'off'
Leaf merge flag, specified as the comma-separated pair consisting of
'MergeLeaves' and 'on' or
'off'.
If MergeLeaves is 'on', then
fitrtree:
Merges leaves that originate from the same parent node and yield a sum of risk values greater than or equal to the risk associated with the parent node
Estimates the optimal sequence of pruned subtrees, but does not prune the regression tree
Otherwise, fitrtree does not
merge leaves.
Example: 'MergeLeaves','off'
MinParentSize — Minimum number of branch node observations
10 (default) | positive integer value
Minimum number of branch node observations, specified as the
comma-separated pair consisting of 'MinParentSize'
and a positive integer value. Each branch node in the tree has at least
MinParentSize observations. If you supply both
MinParentSize and MinLeafSize,
fitrtree uses the setting that gives larger
leaves: MinParentSize =
max(MinParentSize,2*MinLeafSize).
Example: 'MinParentSize',8
Data Types: single | double
NumBins — Number of bins for numeric predictors
[](empty) (default) | positive integer scalar
Number of bins for numeric predictors, specified as the comma-separated pair
consisting of 'NumBins' and a positive integer scalar.
If the
'NumBins'value is empty (default), thenfitrtreedoes not bin any predictors.If you specify the
'NumBins'value as a positive integer scalar (numBins), thenfitrtreebins every numeric predictor into at mostnumBinsequiprobable bins, and then grows trees on the bin indices instead of the original data.The number of bins can be less than
numBinsif a predictor has fewer thannumBinsunique values.fitrtreedoes not bin categorical predictors.
When you use a large training data set, this binning option speeds up training but might cause
a potential decrease in accuracy. You can try 'NumBins',50 first, and
then change the value depending on the accuracy and training speed.
A trained model stores the bin edges in the BinEdges property.
Example: 'NumBins',50
Data Types: single | double
PredictorNames — Predictor variable names
string array of unique names | cell array of unique character vectors
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrtreeuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
PredictorSelection — Algorithm used to select the best split predictor
'allsplits' (default) | 'curvature' | 'interaction-curvature'
Algorithm used to select the best split predictor at each node,
specified as the comma-separated pair consisting of
'PredictorSelection' and a value in this
table.
| Value | Description |
|---|---|
'allsplits' | Standard CART — Selects the split predictor that maximizes the split-criterion gain over all possible splits of all predictors [1]. |
'curvature' | Curvature test — Selects the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response [2]. Training speed is similar to standard CART. |
'interaction-curvature' | Interaction test — Chooses the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response (that is, conducts curvature tests), and that minimizes the p-value of a chi-square test of independence between each pair of predictors and response [2]. Training speed can be slower than standard CART. |
For 'curvature' and
'interaction-curvature', if all tests yield
p-values greater than 0.05, then
fitrtree stops splitting nodes.
Tip
Standard CART tends to select split predictors containing many distinct values, e.g., continuous variables, over those containing few distinct values, e.g., categorical variables [3]. Consider specifying the curvature or interaction test if any of the following are true:
If there are predictors that have relatively fewer distinct values than other predictors, for example, if the predictor data set is heterogeneous.
If an analysis of predictor importance is your goal. For more on predictor importance estimation, see
predictorImportanceand Introduction to Feature Selection.
Trees grown using standard CART are not sensitive to predictor variable interactions. Also, such trees are less likely to identify important variables in the presence of many irrelevant predictors than the application of the interaction test. Therefore, to account for predictor interactions and identify importance variables in the presence of many irrelevant variables, specify the interaction test.
Prediction speed is unaffected by the value of
'PredictorSelection'.
For details on how fitrtree selects split
predictors, see Node Splitting Rules and Choose Split Predictor Selection Technique.
Example: 'PredictorSelection','curvature'
Prune — Flag to estimate optimal sequence of pruned subtrees
'on' (default) | 'off'
Flag to estimate the optimal sequence of pruned subtrees, specified as
the comma-separated pair consisting of 'Prune' and
'on' or 'off'.
If Prune is 'on', then
fitrtree grows the regression tree and
estimates the optimal sequence of pruned subtrees, but does not prune
the regression tree. If Prune is
'off' and MergeLeaves is
also 'off', then fitrtree
grows the regression tree without estimating the optimal sequence of
pruned subtrees.
To prune a trained regression tree, pass the regression tree to
prune.
Example: 'Prune','off'
PruneCriterion — Pruning criterion
'mse' (default)
Pruning criterion, specified as the comma-separated pair consisting of
'PruneCriterion' and
'mse'.
QuadraticErrorTolerance — Quadratic error tolerance
1e-6 (default) | positive scalar value
Quadratic error tolerance per node, specified as the comma-separated
pair consisting of 'QuadraticErrorTolerance' and a
positive scalar value. The function stops splitting nodes when the
weighted mean squared error per node drops below
QuadraticErrorTolerance*ε, where
ε is the weighted mean squared error of all
n responses computed before growing the decision
tree.
wi is the weight of observation i, given that the weights of all the observations sum to one (), and
is the weighted average of all the responses.
For more details on node splitting, see Node Splitting Rules.
Example: 'QuadraticErrorTolerance',1e-4
Reproducible — Flag to enforce reproducibility
false (logical 0) (default) | true (logical 1)
Flag to enforce reproducibility over repeated runs of training a model, specified as the
comma-separated pair consisting of 'Reproducible' and either
false or true.
If 'NumVariablesToSample' is not 'all', then the
software selects predictors at random for each split. To reproduce the random
selections, you must specify 'Reproducible',true and set the seed of
the random number generator by using rng. Note that setting 'Reproducible' to
true can slow down training.
Example: 'Reproducible',true
Data Types: logical
ResponseName — Response variable name
"Y" (default) | character vector | string scalar
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: "ResponseName","response"
Data Types: char | string
ResponseTransform — Function for transforming raw response values
'none' (default) | function handle | function name
Function for transforming raw response values, specified as a function handle or
function name. The default is 'none', which means
@(y)y, or no transformation. The function should accept a vector
(the original response values) and return a vector of the same size (the transformed
response values).
Example: Suppose you create a function handle that applies an exponential
transformation to an input vector by using myfunction = @(y)exp(y).
Then, you can specify the response transformation as
'ResponseTransform',myfunction.
Data Types: char | string | function_handle
SplitCriterion — Split criterion
'MSE' (default)
Split criterion, specified as the comma-separated pair consisting of
'SplitCriterion' and 'MSE',
meaning mean squared error.
Example: 'SplitCriterion','MSE'
Surrogate — Surrogate decision splits flag
'off' (default) | 'on' | 'all' | positive integer
Surrogate decision splits flag, specified as the comma-separated pair
consisting of 'Surrogate' and
'on', 'off',
'all', or a positive integer.
When
'on',fitrtreefinds at most 10 surrogate splits at each branch node.When set to a positive integer,
fitrtreefinds at most the specified number of surrogate splits at each branch node.When set to
'all',fitrtreefinds all surrogate splits at each branch node. The'all'setting can use much time and memory.
Use surrogate splits to improve the accuracy of predictions for data with missing values. The setting also enables you to compute measures of predictive association between predictors.
Example: 'Surrogate','on'
Data Types: single | double | char | string
Weights — Observation weights
ones(size(X,1),1) (default) | vector of scalar values | name of variable in Tbl
Observation weights, specified as the comma-separated pair consisting
of 'Weights' and a vector of scalar values or the
name of a variable in Tbl. The software weights the
observations in each row of X or
Tbl with the corresponding value in
Weights. The size of Weights
must equal the number of rows in X or
Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in
Tbl that contains a numeric vector. In this case,
you must specify Weights as a character vector or
string scalar. For example, if weights vector W is
stored as Tbl.W, then specify it as
'W'. Otherwise, the software treats all columns
of Tbl, including W, as predictors
when training the model.
fitrtree normalizes the values of
Weights to sum to 1.
Data Types: single | double | char | string
CrossVal — Cross-validation flag
'off' (default) | 'on'
Cross-validation flag, specified as the comma-separated pair
consisting of 'CrossVal' and either
'on' or 'off'.
If 'on', fitrtree grows a
cross-validated decision tree with 10 folds. You can override this
cross-validation setting using one of the 'KFold',
'Holdout', 'Leaveout', or
'CVPartition' name-value pair arguments. You can
only use one of these four options ('KFold',
'Holdout', 'Leaveout', or
'CVPartition') at a time when creating a
cross-validated tree.
Alternatively, cross-validate tree later using
the crossval method.
Example: 'CrossVal','on'
CVPartition — Partition for cross-validation tree
cvpartition object
Partition for cross-validated tree, specified as the comma-separated
pair consisting of 'CVPartition' and an object
created using cvpartition.
If you use 'CVPartition', you cannot use any of the
'KFold', 'Holdout', or
'Leaveout' name-value pair arguments.
Holdout — Fraction of data for holdout validation
0 (default) | scalar value in the range [0,1]
Fraction of data used for holdout validation, specified as the
comma-separated pair consisting of 'Holdout' and a
scalar value in the range [0,1]. Holdout validation
tests the specified fraction of the data, and uses the rest of the data
for training.
If you use 'Holdout', you cannot use any of the
'CVPartition', 'KFold', or
'Leaveout' name-value pair arguments.
Example: 'Holdout',0.1
Data Types: single | double
KFold — Number of folds
10 (default) | positive integer greater than 1
Number of folds to use in a cross-validated tree, specified as the
comma-separated pair consisting of 'KFold' and a
positive integer value greater than 1.
If you use 'KFold', you cannot use any of the
'CVPartition', 'Holdout', or
'Leaveout' name-value pair arguments.
Example: 'KFold',8
Data Types: single | double
Leaveout — Leave-one-out cross-validation flag
'off' (default) | 'on'
Leave-one-out cross-validation flag, specified as the comma-separated
pair consisting of 'Leaveout' and either
'on' or 'off. Use
leave-one-out cross-validation by setting to
'on'.
If you use 'Leaveout', you cannot use any of the
'CVPartition', 'Holdout', or
'KFold' name-value pair arguments.
Example: 'Leaveout','on'
MaxNumSplits — Maximal number of decision splits
size(X,1) - 1 (default) | nonnegative scalar
Maximal number of decision splits (or branch nodes), specified as the
comma-separated pair consisting of 'MaxNumSplits' and
a nonnegative scalar. fitrtree splits
MaxNumSplits or fewer branch nodes. For more
details on splitting behavior, see Tree Depth Control.
Example: 'MaxNumSplits',5
Data Types: single | double
MinLeafSize — Minimum number of leaf node observations
1 (default) | positive integer value
Minimum number of leaf node observations, specified as the
comma-separated pair consisting of 'MinLeafSize' and
a positive integer value. Each leaf has at least
MinLeafSize observations per tree leaf. If you
supply both MinParentSize and
MinLeafSize, fitrtree uses
the setting that gives larger leaves: MinParentSize =
max(MinParentSize,2*MinLeafSize).
Example: 'MinLeafSize',3
Data Types: single | double
NumVariablesToSample — Number of predictors to select at random for each split
'all' (default) | positive integer value
Number of predictors to select at random for each split, specified as the comma-separated pair consisting of 'NumVariablesToSample' and a positive integer value. Alternatively, you can specify 'all' to use all available predictors.
If the training data includes many predictors and you want to analyze predictor
importance, then specify 'NumVariablesToSample' as
'all'. Otherwise, the software might not select some predictors,
underestimating their importance.
To reproduce the random selections, you must set the seed of the random number generator by using rng and specify 'Reproducible',true.
Example: 'NumVariablesToSample',3
Data Types: char | string | single | double
OptimizeHyperparameters — Parameters to optimize
'none' (default) | 'auto' | 'all' | string array or cell array of eligible parameter names | vector of optimizableVariable objects
Parameters to optimize, specified as the comma-separated pair
consisting of 'OptimizeHyperparameters' and one of
the following:
'none'— Do not optimize.'auto'— Use{'MinLeafSize'}.'all'— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
The optimization attempts to minimize the cross-validation loss
(error) for fitrtree by varying the parameters.
To control the cross-validation type and other aspects of the
optimization, use the
HyperparameterOptimizationOptions name-value
pair.
Note
The values of OptimizeHyperparameters override any values you specify
using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitrtree to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitrtree
are:
MaxNumSplits—fitrtreesearches among integers, by default log-scaled in the range[1,max(2,NumObservations-1)].MinLeafSize—fitrtreesearches among integers, by default log-scaled in the range[1,max(2,floor(NumObservations/2))].NumVariablesToSample—fitrtreedoes not optimize over this hyperparameter. If you passNumVariablesToSampleas a parameter name,fitrtreesimply uses the full number of predictors. However,fitrensembledoes optimize over this hyperparameter.
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault
values. For example,
load carsmall params = hyperparameters('fitrtree',[Horsepower,Weight],MPG); params(1).Range = [1,30];
Pass params as the value of
OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is log(1 + cross-validation loss). To control the iterative display, set the Verbose field of
the 'HyperparameterOptimizationOptions' name-value argument. To control the
plots, set the ShowPlots field of the
'HyperparameterOptimizationOptions' name-value argument.
For an example, see Optimize Regression Tree.
Example: 'auto'
HyperparameterOptimizationOptions — Options for optimization
structure
Options for optimization, specified as a structure. This argument modifies the effect of the
OptimizeHyperparameters name-value argument. All fields in the
structure are optional.
| Field Name | Values | Default |
|---|---|---|
Optimizer |
| 'bayesopt' |
AcquisitionFunctionName |
Acquisition functions whose names include
| 'expected-improvement-per-second-plus' |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. | 30 for 'bayesopt' and
'randomsearch', and the entire grid for
'gridsearch' |
MaxTime | Time limit, specified as a positive real scalar. The time limit is in seconds, as
measured by | Inf |
NumGridDivisions | For 'gridsearch', the number of values in each dimension. The value can be
a vector of positive integers giving the number of
values for each dimension, or a scalar that
applies to all dimensions. This field is ignored
for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots. If true, this field plots
the best observed objective function value against the iteration number. If you
use Bayesian optimization (Optimizer is
'bayesopt'), then this field also plots the best
estimated objective function value. The best observed objective function values
and best estimated objective function values correspond to the values in the
BestSoFar (observed) and BestSoFar
(estim.) columns of the iterative display, respectively. You can
find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save results when Optimizer is
'bayesopt'. If
true, this field overwrites a
workspace variable named
'BayesoptResults' at each
iteration. The variable is a BayesianOptimization object. | false |
Verbose | Display at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at every
iteration. If this field is The setting
| false |
| Use no more than one of the following three options. | ||
CVPartition | A cvpartition object, as created by cvpartition | 'Kfold',5 if you do not specify a cross-validation
field |
Holdout | A scalar in the range (0,1) representing the holdout fraction | |
Kfold | An integer greater than 1 | |
Example: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)
Data Types: struct
Output Arguments
tree — Regression tree
regression tree object
Regression tree, returned as a regression tree object. Using the
'Crossval', 'KFold',
'Holdout', 'Leaveout', or
'CVPartition' options results in a tree of class
RegressionPartitionedModel. You
cannot use a partitioned tree for prediction, so this kind of tree does not
have a predict method.
Otherwise, tree is of class RegressionTree, and you can use
the predict method to make
predictions.
More About
Curvature Test
The curvature test is a statistical test assessing the null hypothesis that two variables are unassociated.
The curvature test between predictor variable x and y is conducted using this process.
If x is continuous, then partition it into its quartiles. Create a nominal variable that bins observations according to which section of the partition they occupy. If there are missing values, then create an extra bin for them.
For each level in the partitioned predictor j = 1...J and class in the response k = 1,...,K, compute the weighted proportion of observations in class k
wi is the weight of observation i, , I is the indicator function, and n is the sample size. If all observations have the same weight, then , where njk is the number of observations in level j of the predictor that are in class k.
Compute the test statistic
, that is, the marginal probability of observing the predictor at level j. , that is the marginal probability of observing class k. If n is large enough, then t is distributed as a χ2 with (K – 1)(J – 1) degrees of freedom.
If the p-value for the test is less than 0.05, then reject the null hypothesis that there is no association between x and y.
When determining the best split predictor at each node, the standard CART algorithm prefers to select continuous predictors that have many levels. Sometimes, such a selection can be spurious and can also mask more important predictors that have fewer levels, such as categorical predictors.
The curvature test can be applied instead of standard CART to determine the best split predictor at each node. In that case, the best split predictor variable is the one that minimizes the significant p-values (those less than 0.05) of curvature tests between each predictor and the response variable. Such a selection is robust to the number of levels in individual predictors.
For more details on how the curvature test applies to growing regression trees, see Node Splitting Rules and [3].
Interaction Test
The interaction test is a statistical test that assesses the null hypothesis that there is no interaction between a pair of predictor variables and the response variable.
The interaction test assessing the association between predictor variables x1 and x2 with respect to y is conducted using this process.
If x1 or x2 is continuous, then partition that variable into its quartiles. Create a nominal variable that bins observations according to which section of the partition they occupy. If there are missing values, then create an extra bin for them.
Create the nominal variable z with J = J1J2 levels that assigns an index to observation i according to which levels of x1 and x2 it belongs. Remove any levels of z that do not correspond to any observations.
Conduct a curvature test between z and y.
When growing decision trees, if there are important interactions between pairs of predictors, but there are also many other less important predictors in the data, then standard CART tends to miss the important interactions. However, conducting curvature and interaction tests for predictor selection instead can improve detection of important interactions, which can yield more accurate decision trees.
For more details on how the interaction test applies to growing decision trees, see Curvature Test, Node Splitting Rules and [2].
Predictive Measure of Association
The predictive measure of association is a value that indicates the similarity between decision rules that split observations. Among all possible decision splits that are compared to the optimal split (found by growing the tree), the best surrogate decision split yields the maximum predictive measure of association. The second-best surrogate split has the second-largest predictive measure of association.
Suppose xj and xk are predictor variables j and k, respectively, and j ≠ k. At node t, the predictive measure of association between the optimal split xj < u and a surrogate split xk < v is
PL is the proportion of observations in node t, such that xj < u. The subscript L stands for the left child of node t.
PR is the proportion of observations in node t, such that xj ≥ u. The subscript R stands for the right child of node t.
is the proportion of observations at node t, such that xj < u and xk < v.
is the proportion of observations at node t, such that xj ≥ u and xk ≥ v.
Observations with missing values for xj or xk do not contribute to the proportion calculations.
λjk is a value in (–∞,1]. If λjk > 0, then xk < v is a worthwhile surrogate split for xj < u.
Surrogate Decision Splits
A surrogate decision split is an alternative to the optimal decision split at a given node in a decision tree. The optimal split is found by growing the tree; the surrogate split uses a similar or correlated predictor variable and split criterion.
When the value of the optimal split predictor for an observation is missing, the observation is sent to the left or right child node using the best surrogate predictor. When the value of the best surrogate split predictor for the observation is also missing, the observation is sent to the left or right child node using the second-best surrogate predictor, and so on. Candidate splits are sorted in descending order by their predictive measure of association.
Tips
By default,
Pruneis'on'. However, this specification does not prune the regression tree. To prune a trained regression tree, pass the regression tree toprune.After training a model, you can generate C/C++ code that predicts responses for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
Node Splitting Rules
fitrtree uses these processes to determine how to split
node t.
For standard CART (that is, if
PredictorSelectionis'allpairs') and for all predictors xi, i = 1,...,p:fitrtreecomputes the weighted mean squared error (MSE) of the responses in node t usingwj is the weight of observation j, and T is the set of all observation indices in node t. If you do not specify
Weights, then wj = 1/n, where n is the sample size.fitrtreeestimates the probability that an observation is in node t usingfitrtreesorts xi in ascending order. Each element of the sorted predictor is a splitting candidate or cut point.fitrtreerecords any indices corresponding to missing values in the set TU, which is the unsplit set.fitrtreedetermines the best way to split node t using xi by maximizing the reduction in MSE (ΔI) over all splitting candidates. That is, for all splitting candidates in xi:fitrtreesplits the observations in node t into left and right child nodes (tL and tR, respectively).fitrtreecomputes ΔI. Suppose that for a particular splitting candidate, tL and tR contain observation indices in the sets TL and TR, respectively.If xi does not contain any missing values, then the reduction in MSE for the current splitting candidate is
If xi contains missing values, then, assuming that the observations are missing at random, the reduction in MSE is
T – TU is the set of all observation indices in node t that are not missing.
If you use surrogate decision splits, then:
fitrtreecomputes the predictive measures of association between the decision split xj < u and all possible decision splits xk < v, j ≠ k.fitrtreesorts the possible alternative decision splits in descending order by their predictive measure of association with the optimal split. The surrogate split is the decision split yielding the largest measure.fitrtreedecides the child node assignments for observations with a missing value for xi using the surrogate split. If the surrogate predictor also contains a missing value, thenfitrtreeuses the decision split with the second largest measure, and so on, until there are no other surrogates. It is possible forfitrtreeto split two different observations at node t using two different surrogate splits. For example, suppose the predictors x1 and x2 are the best and second best surrogates, respectively, for the predictor xi, i ∉ {1,2}, at node t. If observation m of predictor xi is missing (i.e., xmi is missing), but xm1 is not missing, then x1 is the surrogate predictor for observation xmi. If observations x(m + 1),i and x(m + 1),1 are missing, but x(m + 1),2 is not missing, then x2 is the surrogate predictor for observation m + 1.fitrtreeuses the appropriate MSE reduction formula. That is, iffitrtreefails to assign all missing observations in node t to children nodes using surrogate splits, then the MSE reduction is ΔIU. Otherwise,fitrtreeuses ΔI for the MSE reduction.
fitrtreechooses the candidate that yields the largest MSE reduction.
fitrtreesplits the predictor variable at the cut point that maximizes the MSE reduction.For the curvature test (that is, if
PredictorSelectionis'curvature'):fitrtreecomputes the residuals for all observations in node t. , which is the weighted average of the responses in node t. The weights are the observation weights inWeights.fitrtreeassigns observations to one of two bins according to the sign of the corresponding residuals. Let zt be a nominal variable that contains the bin assignments for the observations in node t.fitrtreeconducts curvature tests between each predictor and zt. For regression trees, K = 2.If all p-values are at least 0.05, then
fitrtreedoes not split node t.If there is a minimal p-value, then
fitrtreechooses the corresponding predictor to split node t.If more than one p-value is zero due to underflow, then
fitrtreeapplies standard CART to the corresponding predictors to choose the split predictor.
If
fitrtreechooses a split predictor, then it uses standard CART to choose the cut point (see step 4 in the standard CART process).
For the interaction test (that is, if
PredictorSelectionis'interaction-curvature'):For observations in node t,
fitrtreeconducts curvature tests between each predictor and the response and interaction tests between each pair of predictors and the response.If all p-values are at least 0.05, then
fitrtreedoes not split node t.If there is a minimal p-value and it is the result of a curvature test, then
fitrtreechooses the corresponding predictor to split node t.If there is a minimal p-value and it is the result of an interaction test, then
fitrtreechooses the split predictor using standard CART on the corresponding pair of predictors.If more than one p-value is zero due to underflow, then
fitrtreeapplies standard CART to the corresponding predictors to choose the split predictor.
If
fitrtreechooses a split predictor, then it uses standard CART to choose the cut point (see step 4 in the standard CART process).
Tree Depth Control
If
MergeLeavesis'on'andPruneCriterionis'mse'(which are the default values for these name-value pair arguments), then the software applies pruning only to the leaves and by using MSE. This specification amounts to merging leaves coming from the same parent node whose MSE is at most the sum of the MSE of its two leaves.To accommodate
MaxNumSplits,fitrtreesplits all nodes in the current layer, and then counts the number of branch nodes. A layer is the set of nodes that are equidistant from the root node. If the number of branch nodes exceedsMaxNumSplits,fitrtreefollows this procedure:Determine how many branch nodes in the current layer must be unsplit so that there are at most
MaxNumSplitsbranch nodes.Sort the branch nodes by their impurity gains.
Unsplit the number of least successful branches.
Return the decision tree grown so far.
This procedure produces maximally balanced trees.
The software splits branch nodes layer by layer until at least one of these events occurs:
There are
MaxNumSplitsbranch nodes.A proposed split causes the number of observations in at least one branch node to be fewer than
MinParentSize.A proposed split causes the number of observations in at least one leaf node to be fewer than
MinLeafSize.The algorithm cannot find a good split within a layer (i.e., the pruning criterion (see
PruneCriterion), does not improve for all proposed splits in a layer). A special case is when all nodes are pure (i.e., all observations in the node have the same class).For values
'curvature'or'interaction-curvature'ofPredictorSelection, all tests yield p-values greater than 0.05.
MaxNumSplitsandMinLeafSizedo not affect splitting at their default values. Therefore, if you set'MaxNumSplits', splitting might stop due to the value ofMinParentSize, beforeMaxNumSplitssplits occur.
Parallelization
For dual-core systems and above, fitrtree parallelizes
training decision trees using Intel® Threading Building Blocks (TBB). For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.
References
[1] Breiman, L., J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Boca Raton, FL: CRC Press, 1984.
[2] Loh, W.Y. “Regression Trees with Unbiased Variable Selection and Interaction Detection.” Statistica Sinica, Vol. 12, 2002, pp. 361–386.
[3] Loh, W.Y. and Y.S. Shih. “Split Selection Methods for Classification Trees.” Statistica Sinica, Vol. 7, 1997, pp. 815–840.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Usage notes and limitations:
Supported syntaxes are:
tree = fitrtree(Tbl,Y)tree = fitrtree(X,Y)tree = fitrtree(___,Name,Value)[tree,FitInfo,HyperparameterOptimizationResults] = fitrtree(___,Name,Value)—fitrtreereturns the additional output argumentsFitInfoandHyperparameterOptimizationResultswhen you specify the'OptimizeHyperparameters'name-value pair argument.
treeis aCompactRegressionTreeobject; therefore, it does not include the data used in training the regression tree.The
FitInfooutput argument is an empty structure array currently reserved for possible future use.The
HyperparameterOptimizationResultsoutput argument is aBayesianOptimizationobject or a table of hyperparameters with associated values that describe the cross-validation optimization of hyperparameters.'HyperparameterOptimizationResults'is nonempty when the'OptimizeHyperparameters'name-value pair argument is nonempty at the time you create the model. The values in'HyperparameterOptimizationResults'depend on the value you specify for the'HyperparameterOptimizationOptions'name-value pair argument when you create the model.If you specify
'bayesopt'(default), thenHyperparameterOptimizationResultsis an object of classBayesianOptimization.If you specify
'gridsearch'or'randomsearch', thenHyperparameterOptimizationResultsis a table of the hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst).
Supported name-value pair arguments are:
'CategoricalPredictors''HyperparameterOptimizationOptions'— For cross-validation, tall optimization supports only'Holdout'validation. By default, the software selects and reserves 20% of the data as holdout validation data, and trains the model using the rest of the data. You can specify a different value for the holdout fraction by using this argument. For example, specify'HyperparameterOptimizationOptions',struct('Holdout',0.3)to reserve 30% of the data as validation data.'MaxNumSplits'— For tall optimization,fitrtreesearches among integers, log-scaled (by default) in the range[1,max(2,min(10000,NumObservations–1))].'MergeLeaves''MinLeafSize'— For tall optimization,fitrtreesearches among integers, log-scaled (by default) in the range[1,max(2,floor(NumObservations/2))].'MinParentSize''NumVariablesToSample'— For tall optimization,fitrtreesearches among integers in the range[1,max(2,NumPredictors)].'OptimizeHyperparameters''PredictorNames''QuadraticErrorTolerance''ResponseName''ResponseTransform''SplitCriterion''Weights'
This additional name-value pair argument is specific to tall arrays:
'MaxDepth'— A positive integer specifying the maximum depth of the output tree. Specify a value for this argument to return a tree that has fewer levels and requires fewer passes through the tall array to compute. Generally, the algorithm offitrtreetakes one pass through the data and an additional pass for each tree level. The function does not set a maximum tree depth, by default.
For more information, see Tall Arrays.
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To perform parallel hyperparameter optimization, use the
'HyperparameterOptimizationOptions', struct('UseParallel',true)
name-value argument in the call to the fitrtree function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
fitrtreedoes not support surrogate splits. You can specify the name-value argumentSurrogateonly as"off".For data with categorical predictors, you can specify the name-value argument
NumVariablesToSampleonly as"all".You can specify the name-value argument
PredictorSelectiononly as"allsplits".fitrtreefits the model on a GPU if any of the following apply:The input argument
Xis agpuArrayobject.The input argument
Yis agpuArrayobject.The input argument
TblcontainsgpuArraypredictor or response variables.
Note that
fitrtreemight not execute faster on a GPU than a CPU for deeper decision trees.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2014a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)