pca
Principal component analysis of raw data
Syntax
Description
coeff = pca(X)X. The rows of
X correspond to observations, and the columns correspond to variables.
Each column of the coefficient matrix coeff contains the coefficients for
one principal component. The columns are sorted in descending order by principal component
variance. By default, pca centers the data and uses the singular value
decomposition (SVD) algorithm.
coeff = pca(X,Name,Value)Name,Value pair arguments.
For example, you can specify the number of principal components pca returns
or an algorithm other than SVD to use.
[ also returns the principal component
scores in coeff,score,latent]
= pca(___)score and the principal component variances
in latent. You can use any of the input arguments
in the previous syntaxes.
Principal component scores are the representations of X in
the principal component space. Rows of score correspond
to observations, and columns correspond to components.
The principal component variances are the eigenvalues of the
covariance matrix of X.
Examples
Load the sample data set.
load haldThe ingredients data has 13 observations for 4 variables.
Find the principal components for the ingredients data.
coeff = pca(ingredients)
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
The rows of coeff contain the coefficients for the four ingredient variables, and its columns correspond to four principal components.
Find the principal component coefficients when there are missing values in a data set.
Load the sample data set.
load imports-85Data matrix X has 13 continuous variables
in columns 3 to 15: wheel-base, length, width, height, curb-weight,
engine-size, bore, stroke, compression-ratio, horsepower, peak-rpm,
city-mpg, and highway-mpg. The variables bore and stroke are missing
four values in rows 56 to 59, and the variables horsepower and peak-rpm
are missing two values in rows 131 and 132.
Perform principal component analysis.
coeff = pca(X(:,3:15));
By default, pca performs the action specified
by the 'Rows','complete' name-value pair argument.
This option removes the observations with NaN values
before calculation. Rows of NaNs are reinserted
into score and tsquared at the
corresponding locations, namely rows 56 to 59, 131, and 132.
Use 'pairwise' to perform the principal
component analysis.
coeff = pca(X(:,3:15),'Rows','pairwise');
In this case, pca computes the (i,j)
element of the covariance matrix using the rows with no NaN values
in the columns i or j of X.
Note that the resulting covariance matrix might not be positive definite.
This option applies when the algorithm pca uses
is eigenvalue decomposition. When you don’t specify the algorithm,
as in this example, pca sets it to 'eig'.
If you require 'svd' as the algorithm, with the 'pairwise' option,
then pca returns a warning message, sets the algorithm
to 'eig' and continues.
If you use the 'Rows','all' name-value
pair argument, pca terminates because this option
assumes there are no missing values in the data set.
coeff = pca(X(:,3:15),'Rows','all');
Error using pca (line 180) Raw data contains NaN missing value while 'Rows' option is set to 'all'. Consider using 'complete' or pairwise' option instead.
Use the inverse variable variances as weights while performing the principal components analysis.
Load the sample data set.
load haldPerform the principal component analysis using the inverse of variances of the ingredients as variable weights.
[wcoeff,~,latent,~,explained] = pca(ingredients,'VariableWeights','variance')
wcoeff = 4×4
-2.7998 2.9940 -3.9736 1.4180
-8.7743 -6.4411 4.8927 9.9863
2.5240 -3.8749 -4.0845 1.7196
9.1714 7.5529 3.2710 11.3273
latent = 4×1
2.2357
1.5761
0.1866
0.0016
explained = 4×1
55.8926
39.4017
4.6652
0.0406
Note that the coefficient matrix wcoeff is not orthonormal.
Calculate the orthonormal coefficient matrix.
coefforth = diag(std(ingredients))\wcoeff
coefforth = 4×4
-0.4760 0.5090 -0.6755 0.2411
-0.5639 -0.4139 0.3144 0.6418
0.3941 -0.6050 -0.6377 0.2685
0.5479 0.4512 0.1954 0.6767
Check orthonormality of the new coefficient matrix, coefforth.
coefforth*coefforth'
ans = 4×4
1.0000 0.0000 -0.0000 0.0000
0.0000 1.0000 -0.0000 -0.0000
-0.0000 -0.0000 1.0000 0.0000
0.0000 -0.0000 0.0000 1.0000
Find the principal components using the alternating least squares (ALS) algorithm when there are missing values in the data.
Load the sample data.
load haldThe ingredients data has 13 observations for 4 variables.
Perform principal component analysis using the ALS algorithm and display the component coefficients.
[coeff,score,latent,tsquared,explained] = pca(ingredients); coeff
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
Introduce missing values randomly.
y = ingredients; rng('default'); % for reproducibility ix = random('unif',0,1,size(y))<0.30; y(ix) = NaN
y = 13×4
7 26 6 NaN
1 29 15 52
NaN NaN 8 20
11 31 NaN 47
7 52 6 33
NaN 55 NaN NaN
NaN 71 NaN 6
1 31 NaN 44
2 NaN NaN 22
21 47 4 26
NaN 40 23 34
11 66 9 NaN
10 68 8 12
⋮
Approximately 30% of the data has missing values now, indicated by NaN.
Perform principal component analysis using the ALS algorithm and display the component coefficients.
[coeff1,score1,latent,tsquared,explained,mu1] = pca(y,... 'algorithm','als'); coeff1
coeff1 = 4×4
-0.0362 0.8215 -0.5252 0.2190
-0.6831 -0.0998 0.1828 0.6999
0.0169 0.5575 0.8215 -0.1185
0.7292 -0.0657 0.1261 0.6694
Display the estimated mean.
mu1
mu1 = 1×4
8.9956 47.9088 9.0451 28.5515
Reconstruct the observed data.
t = score1*coeff1' + repmat(mu1,13,1)
t = 13×4
7.0000 26.0000 6.0000 51.5250
1.0000 29.0000 15.0000 52.0000
10.7819 53.0230 8.0000 20.0000
11.0000 31.0000 13.5500 47.0000
7.0000 52.0000 6.0000 33.0000
10.4818 55.0000 7.8328 17.9362
3.0982 71.0000 11.9491 6.0000
1.0000 31.0000 -0.5161 44.0000
2.0000 53.7914 5.7710 22.0000
21.0000 47.0000 4.0000 26.0000
21.5809 40.0000 23.0000 34.0000
11.0000 66.0000 9.0000 5.7078
10.0000 68.0000 8.0000 12.0000
⋮
The ALS algorithm estimates the missing values in the data.
Another way to compare the results is to find the angle between the two spaces spanned by the coefficient vectors. Find the angle between the coefficients found for complete data and data with missing values using ALS.
subspace(coeff,coeff1)
ans = 7.3147e-16
This is a small value. It indicates that the results if you use pca with 'Rows','complete' name-value pair argument when there is no missing data and if you use pca with 'algorithm','als' name-value pair argument when there is missing data are close to each other.
Perform the principal component analysis using 'Rows','complete' name-value pair argument and display the component coefficients.
[coeff2,score2,latent,tsquared,explained,mu2] = pca(y,... 'Rows','complete'); coeff2
coeff2 = 4×3
-0.2054 0.8587 0.0492
-0.6694 -0.3720 0.5510
0.1474 -0.3513 -0.5187
0.6986 -0.0298 0.6518
In this case, pca removes the rows with missing values, and y has only four rows with no missing values. pca returns only three principal components. You cannot use the 'Rows','pairwise' option because the covariance matrix is not positive semidefinite and pca returns an error message.
Find the angle between the coefficients found for complete data and data with missing values using listwise deletion (when 'Rows','complete').
subspace(coeff(:,1:3),coeff2)
ans = 0.3576
The angle between the two spaces is substantially larger. This indicates that these two results are different.
Display the estimated mean.
mu2
mu2 = 1×4
7.8889 46.9091 9.8750 29.6000
In this case, the mean is just the sample mean of y.
Reconstruct the observed data.
score2*coeff2'
ans = 13×4
NaN NaN NaN NaN
-7.5162 -18.3545 4.0968 22.0056
NaN NaN NaN NaN
NaN NaN NaN NaN
-0.5644 5.3213 -3.3432 3.6040
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN
NaN NaN NaN NaN
12.8315 -0.1076 -6.3333 -3.7758
NaN NaN NaN NaN
NaN NaN NaN NaN
1.4680 20.6342 -2.9292 -18.0043
⋮
This shows that deleting rows containing NaN values does not work as well as the ALS algorithm. Using ALS is better when the data has too many missing values.
Find the coefficients, scores, and variances of the principal components.
Load the sample data set.
load haldThe ingredients data has 13 observations for 4 variables.
Find the principal component coefficients, scores, and variances of the components for the ingredients data.
[coeff,score,latent] = pca(ingredients)
coeff = 4×4
-0.0678 -0.6460 0.5673 0.5062
-0.6785 -0.0200 -0.5440 0.4933
0.0290 0.7553 0.4036 0.5156
0.7309 -0.1085 -0.4684 0.4844
score = 13×4
36.8218 -6.8709 -4.5909 0.3967
29.6073 4.6109 -2.2476 -0.3958
-12.9818 -4.2049 0.9022 -1.1261
23.7147 -6.6341 1.8547 -0.3786
-0.5532 -4.4617 -6.0874 0.1424
-10.8125 -3.6466 0.9130 -0.1350
-32.5882 8.9798 -1.6063 0.0818
22.6064 10.7259 3.2365 0.3243
-9.2626 8.9854 -0.0169 -0.5437
-3.2840 -14.1573 7.0465 0.3405
9.2200 12.3861 3.4283 0.4352
-25.5849 -2.7817 -0.3867 0.4468
-26.9032 -2.9310 -2.4455 0.4116
⋮
latent = 4×1
517.7969
67.4964
12.4054
0.2372
Each column of score corresponds to one principal component. The vector, latent, stores the variances of the four principal components.
Reconstruct the centered ingredients data.
Xcentered = score*coeff'
Xcentered = 13×4
-0.4615 -22.1538 -5.7692 30.0000
-6.4615 -19.1538 3.2308 22.0000
3.5385 7.8462 -3.7692 -10.0000
3.5385 -17.1538 -3.7692 17.0000
-0.4615 3.8462 -5.7692 3.0000
3.5385 6.8462 -2.7692 -8.0000
-4.4615 22.8462 5.2308 -24.0000
-6.4615 -17.1538 10.2308 14.0000
-5.4615 5.8462 6.2308 -8.0000
13.5385 -1.1538 -7.7692 -4.0000
-6.4615 -8.1538 11.2308 4.0000
3.5385 17.8462 -2.7692 -18.0000
2.5385 19.8462 -3.7692 -18.0000
⋮
The new data in Xcentered is the original ingredients data centered by subtracting the column means from corresponding columns.
Visualize both the orthonormal principal component coefficients for each variable and the principal component scores for each observation in a single plot.
biplot(coeff(:,1:2),'scores',score(:,1:2),'varlabels',{'v_1','v_2','v_3','v_4'});
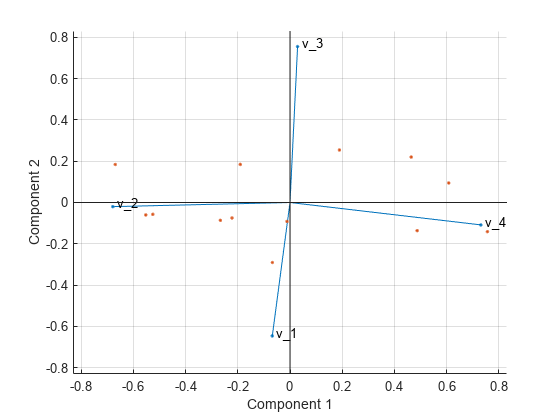
All four variables are represented in this biplot by a vector, and the direction and length of the vector indicate how each variable contributes to the two principal components in the plot. For example, the first principal component, which is on the horizontal axis, has positive coefficients for the third and fourth variables. Therefore, vectors and are directed into the right half of the plot. The largest coefficient in the first principal component is the fourth, corresponding to the variable .
The second principal component, which is on the vertical axis, has negative coefficients for the variables , , and , and a positive coefficient for the variable .
This 2-D biplot also includes a point for each of the 13 observations, with coordinates indicating the score of each observation for the two principal components in the plot. For example, points near the left edge of the plot have the lowest scores for the first principal component. The points are scaled with respect to the maximum score value and maximum coefficient length, so only their relative locations can be determined from the plot.
Find the Hotelling’s T-squared statistic values.
Load the sample data set.
load haldThe ingredients data has 13 observations for 4 variables.
Perform the principal component analysis and request the T-squared values.
[coeff,score,latent,tsquared] = pca(ingredients); tsquared
tsquared = 13×1
5.6803
3.0758
6.0002
2.6198
3.3681
0.5668
3.4818
3.9794
2.6086
7.4818
4.1830
2.2327
2.7216
⋮
Request only the first two principal components and compute the T-squared values in the reduced space of requested principal components.
[coeff,score,latent,tsquared] = pca(ingredients,'NumComponents',2);
tsquaredtsquared = 13×1
5.6803
3.0758
6.0002
2.6198
3.3681
0.5668
3.4818
3.9794
2.6086
7.4818
4.1830
2.2327
2.7216
⋮
Note that even when you specify a reduced component space, pca computes the T-squared values in the full space, using all four components.
The T-squared value in the reduced space corresponds to the Mahalanobis distance in the reduced space.
tsqreduced = mahal(score,score)
tsqreduced = 13×1
3.3179
2.0079
0.5874
1.7382
0.2955
0.4228
3.2457
2.6914
1.3619
2.9903
2.4371
1.3788
1.5251
⋮
Calculate the T-squared values in the discarded space by taking the difference of the T-squared values in the full space and Mahalanobis distance in the reduced space.
tsqdiscarded = tsquared - tsqreduced
tsqdiscarded = 13×1
2.3624
1.0679
5.4128
0.8816
3.0726
0.1440
0.2362
1.2880
1.2467
4.4915
1.7459
0.8539
1.1965
⋮
Find the percent variability explained by the principal components. Show the data representation in the principal components space.
Load the sample data set.
load imports-85Data matrix X has 13 continuous variables in columns 3 to 15: wheel-base, length, width, height, curb-weight, engine-size, bore, stroke, compression-ratio, horsepower, peak-rpm, city-mpg, and highway-mpg.
Find the percent variability explained by principal components of these variables.
[coeff,score,latent,tsquared,explained] = pca(X(:,3:15)); explained
explained = 13×1
64.3429
35.4484
0.1550
0.0379
0.0078
0.0048
0.0013
0.0011
0.0005
0.0002
0.0002
0.0000
0.0000
⋮
The first three components explain 99.95% of all variability.
Visualize the data representation in the space of the first three principal components.
scatter3(score(:,1),score(:,2),score(:,3)) axis equal xlabel('1st Principal Component') ylabel('2nd Principal Component') zlabel('3rd Principal Component')
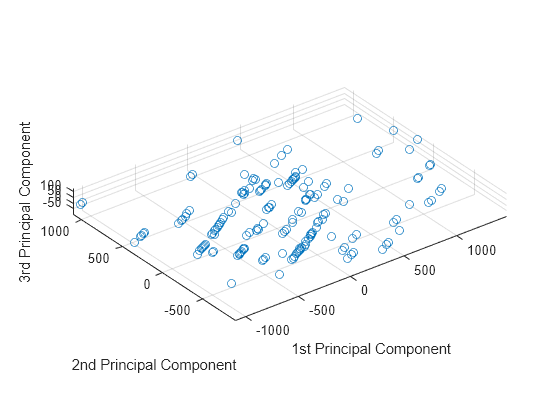
The data shows the largest variability along the first principal component axis. This is the largest possible variance among all possible choices of the first axis. The variability along the second principal component axis is the largest among all possible remaining choices of the second axis. The third principal component axis has the third largest variability, which is significantly smaller than the variability along the second principal component axis. The fourth through thirteenth principal component axes are not worth inspecting, because they explain only 0.05% of all variability in the data.
To skip any of the outputs, you can use ~ instead in the corresponding element. For example, if you don’t want to get the T-squared values, specify
[coeff,score,latent,~,explained] = pca(X(:,3:15));
Find the principal components for one data set and apply the PCA to another data set. This procedure is useful when you have a training data set and a test data set for a machine learning model. For example, you can preprocess the training data set by using PCA and then train a model. To test the trained model using the test data set, you need to apply the PCA transformation obtained from the training data to the test data set.
This example also describes how to generate C/C++ code. Because pca supports code generation, you can generate code that performs PCA using a training data set and applies the PCA to a test data set. Then deploy the code to a device. In this workflow, you must pass training data, which can be of considerable size. To save memory on the device, you can separate training and prediction. Use pca in MATLAB® and apply PCA to new data in the generated code on the device.
Generating C/C++ code requires MATLAB® Coder™.
Apply PCA to New Data
Load the data set into a table by using readtable. The data set is in the file CreditRating_Historical.dat, which contains the historical credit rating data.
creditrating = readtable('CreditRating_Historical.dat');
creditrating(1:5,:)ans=5×8 table
ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ _____ _____ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
The first column is an ID of each observation, and the last column is a rating. Specify the second to seventh columns as predictor data and specify the last column (Rating) as the response.
X = table2array(creditrating(:,2:7)); Y = creditrating.Rating;
Use the first 100 observations as test data and the rest as training data.
XTest = X(1:100,:); XTrain = X(101:end,:); YTest = Y(1:100); YTrain = Y(101:end);
Find the principal components for the training data set XTrain.
[coeff,scoreTrain,~,~,explained,mu] = pca(XTrain);
This code returns four outputs: coeff, scoreTrain, explained, and mu. Use explained (percentage of total variance explained) to find the number of components required to explain at least 95% variability. Use coeff (principal component coefficients) and mu (estimated means of XTrain) to apply the PCA to a test data set. Use scoreTrain (principal component scores) instead of XTrain when you train a model.
Display the percent variability explained by the principal components.
explained
explained = 6×1
58.2614
41.2606
0.3875
0.0632
0.0269
0.0005
The first two components explain more than 95% of all variability. Find the number of components required to explain at least 95% variability.
idx = find(cumsum(explained)>95,1)
idx = 2
Train a classification tree using the first two components.
scoreTrain95 = scoreTrain(:,1:idx); mdl = fitctree(scoreTrain95,YTrain);
mdl is a ClassificationTree model.
To use the trained model for the test set, you need to transform the test data set by using the PCA obtained from the training data set. Obtain the principal component scores of the test data set by subtracting mu from XTest and multiplying by coeff. Only the scores for the first two components are necessary, so use the first two coefficients coeff(:,1:idx).
scoreTest95 = (XTest-mu)*coeff(:,1:idx);
Pass the trained model mdl and the transformed test data set scoreTest to the predict function to predict ratings for the test set.
YTest_predicted = predict(mdl,scoreTest95);
Generate Code
Generate code that applies PCA to data and predicts ratings using the trained model. Note that generating C/C++ code requires MATLAB® Coder™.
Save the classification model to the file myMdl.mat by using saveLearnerForCoder.
saveLearnerForCoder(mdl,'myMdl');Define an entry-point function named myPCAPredict that accepts a test data set (XTest) and PCA information (coeff and mu) and returns the ratings of the test data.
Add the %#codegen compiler directive (or pragma) to the entry-point function after the function signature to indicate that you intend to generate code for the MATLAB algorithm. Adding this directive instructs the MATLAB Code Analyzer to help you diagnose and fix violations that would cause errors during code generation.
function label = myPCAPredict(XTest,coeff,mu) %#codegen % Transform data using PCA scoreTest = bsxfun(@minus,XTest,mu)*coeff; % Load trained classification model mdl = loadLearnerForCoder('myMdl'); % Predict ratings using the loaded model label = predict(mdl,scoreTest);
myPCAPredict applies PCA to new data using coeff and mu, and then predicts ratings using the transformed data. In this way, you do not pass training data, which can be of considerable size.
Note: If you click the button located in the upper-right section of this page and open this example in MATLAB®, then MATLAB® opens the example folder. This folder includes the entry-point function file.
Generate code by using codegen (MATLAB Coder). Because C and C++ are statically typed languages, you must determine the properties of all variables in the entry-point function at compile time. To specify the data type and exact input array size, pass a MATLAB® expression that represents the set of values with a certain data type and array size by using the -args option. If the number of observations is unknown at compile time, you can also specify the input as variable-size by using coder.typeof (MATLAB Coder). For details, see Specify Variable-Size Arguments for Code Generation.
codegen myPCAPredict -args {coder.typeof(XTest,[Inf,6],[1,0]),coeff(:,1:idx),mu}
Code generation successful.
codegen generates the MEX function myPCAPredict_mex with a platform-dependent extension.
Verify the generated code.
YTest_predicted_mex = myPCAPredict_mex(XTest,coeff(:,1:idx),mu); isequal(YTest_predicted,YTest_predicted_mex)
ans = logical
1
isequal returns logical 1 (true), which means all the inputs are equal. The comparison confirms that the predict function of mdl and the myPCAPredict_mex function return the same ratings.
For more information on code generation, see Introduction to Code Generationand Generate Code at Command Line Using Model Exported from Machine Learning App. The latter describes how to perform PCA and train a model by using the Classification Learner app, and how to generate C/C++ code that predicts labels for new data based on the trained model.
Input Arguments
Input data for which to compute the principal components, specified
as an n-by-p matrix. Rows of X correspond
to observations and columns to variables.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Algorithm','eig','Centered','off','Rows','all','NumComponents',3
specifies that pca uses eigenvalue decomposition algorithm, not center
the data, use all of the observations, and return only the first three principal
components.
Principal component algorithm that pca uses
to perform the principal component analysis, specified as the comma-separated
pair consisting of 'Algorithm' and one of the following.
| Value | Description |
|---|---|
'svd' | Default. Singular value decomposition (SVD) of X. |
'eig' | Eigenvalue decomposition (EIG) of the covariance matrix. The
EIG algorithm is faster than SVD when the number of observations, n,
exceeds the number of variables, p, but is less
accurate because the condition number of the covariance is the square
of the condition number of X. |
'als' |
Alternating least squares (ALS) algorithm. This
algorithm finds the best rank- ALS is designed to better handle missing values.
It is preferable to pairwise deletion
( |
Example: 'Algorithm','eig'
Indicator for centering the columns, specified as the comma-separated
pair consisting of 'Centered' and one of these
logical expressions.
| Value | Description |
|---|---|
on | Default. |
off | In this case |
Example: 'Centered',off
Data Types: logical
Indicator for the economy size output when the degrees of freedom, d,
is smaller than the number of variables, p, specified
as the comma-separated pair consisting of 'Economy' and
one of these logical expressions.
| Value | Description |
|---|---|
true | Default. This option can be significantly faster when the number of variables p is much larger than d. |
false |
|
Note that when d < p, score(:,d+1:p) and latent(d+1:p) are
necessarily zero, and the columns of coeff(:,d+1:p) define
directions that are orthogonal to X.
Example: 'Economy',false
Data Types: logical
Action to take for NaN values in the data
matrix X, specified as the comma-separated pair
consisting of 'Rows' and one of the following.
| Value | Description |
|---|---|
'complete' | Default. If an observation in |
'pairwise' | This option only applies when the algorithm is When you specify the Note
that the resulting covariance matrix might not be positive definite.
In that case, |
'all' |
|
Example: 'Rows','pairwise'
Observation weights, specified as the comma-separated pair
consisting of 'Weights' and a vector of length n containing
all positive elements.
Data Types: single | double
Variable weights,
specified as the comma-separated pair consisting of 'VariableWeights' and
one of the following.
| Value | Description |
|---|---|
row vector | Vector of length p containing all positive elements. |
'variance' | The variable weights are the inverse of sample variance. If you also assign weights to
observations using If
|
Example: 'VariableWeights','variance'
Data Types: single | double | char | string
Initial value for the coefficient matrix coeff,
specified as the comma-separated pair consisting of 'Coeff0' and
a p-by-k matrix, where p is
the number of variables, and k is the number of
principal components requested.
Note
You can use this name-value pair only when 'algorithm' is 'als'.
Data Types: single | double
Initial value for scores matrix score,
specified as a comma-separated pair consisting of 'Score0' and
an n-by-k matrix, where n is
the number of observations and k is the number
of principal components requested.
Note
You can use this name-value pair only when 'algorithm' is 'als'.
Data Types: single | double
Options for the iterations, specified as a comma-separated pair
consisting of 'Options' and a structure created
by the statset function. pca uses
the following fields in the options structure.
| Field Name | Description |
|---|---|
'Display' | Level of display output. Choices are 'off', 'final',
and 'iter'. |
'MaxIter' | Maximum number steps allowed. The default is 1000. Unlike in
optimization settings, reaching the MaxIter value
is regarded as convergence. |
'TolFun' | Positive number giving the termination tolerance for the cost function. The default is 1e-6. |
'TolX' | Positive number giving the convergence threshold for the relative change in the elements of the left and right factor matrices, L and R, in the ALS algorithm. The default is 1e-6. |
Note
You can use this name-value pair only when 'algorithm' is 'als'.
You can change the values of these fields and specify the new
structure in pca using the 'Options' name-value
pair argument.
Example: opt = statset('pca'); opt.MaxIter = 2000; coeff
= pca(X,'Options',opt);
Data Types: struct
Output Arguments
Principal component coefficients, returned as a
p-by-k numeric matrix, where
p=size(X,2). If X is a tall array,
coeff is a p-by-p numeric
matrix. For more information, see Tall Arrays.
When you specify NumComponents, the following
conditions apply:
If you specify
Economy=true(default), thenkequalsmin(NumComponents,d), wheredis the number of degrees of freedom.If you specify
Economy=falseandNumComponents < d, thenkequalsNumComponents.If you specify
Economy=falseandNumComponents ≥ d, thenkequalsp.
When you do not specify NumComponents, the following
conditions apply:
If you specify
Economy=true(default), thenkequals the number of degrees of freedom.If you specify
Economy=false, thenkequalsp.
Each column of coeff contains the coefficients for one
principal component. The columns are arranged in descending order by principal component
variance (see latent).
Principal component scores, returned as an n-by-k
numeric matrix, where n=size(X,1).
When you specify NumComponents, the following conditions apply:
If you specify
Economy=true(default), thenkequalsmin(NumComponents,d), wheredis the number of degrees of freedom.If you specify
Economy=falseandNumComponents < d, thenkequalsNumComponents.If you specify
Economy=falseandNumComponents ≥ d, thenkequalssize(X,2).
When you do not specify NumComponents, the following
conditions apply:
If you specify
Economy=true(default), thenkequals the number of degrees of freedom.If you specify
Economy=false, thenkequalssize(X,2).
The rows of score correspond to observations, and the
columns correspond to components.
Principal component variances, namely the eigenvalues of the covariance matrix of
X, returned as a numeric column vector of length
k.
If the number of degrees of freedom is smaller
than size(X,2) and you specify Economy=true (default), then k
equals the number of degrees of freedom. Otherwise, k equals
size(X,2).
Hotelling’s T-Squared Statistic, which is the sum of squares of the
standardized scores for each observation, returned as a numeric column vector of length
size(X,2).
Percentage of the total variance explained by each principal component, returned as a numeric
column vector of length k.
If the number of degrees of freedom is smaller
than size(X,2) and you specify Economy=true (default), then k
equals the number of degrees of freedom. Otherwise, k equals
size(X,2).
More About
Hotelling’s T-squared statistic is a statistical measure of the multivariate distance of each observation from the center of the data set.
Even when you request fewer components than the number of variables, pca uses
all principal components to compute the T-squared statistic (computes
it in the full space). If you want the T-squared statistic in the
reduced or the discarded space, do one of the following:
For the T-squared statistic in the reduced space, use
mahal(score,score).For the T-squared statistic in the discarded space, first compute the T-squared statistic using
[coeff,score,latent,tsquared] = pca(X,'NumComponents',k,...), compute the T-squared statistic in the reduced space usingtsqreduced = mahal(score,score), and then take the difference:tsquared-tsqreduced.
The degrees of freedom d is equal to i – 1 if data is centered, and i otherwise.
If you specify
'Rows','complete', i is the number of rows inXwithout anyNaNs.If you specify
'Rows','pairwise', i is the number of rows inXwithout anyNaNs in the column pair that has the maximum number of rows withoutNaNs.
Note that when variable weights are used, the
coefficient matrix is not orthonormal. Suppose the variable weights
vector you used is called varwei, and the principal
component coefficients vector pca returned is wcoeff.
You can then calculate the orthonormal coefficients using the transformation diag(sqrt(varwei))*wcoeff.
Algorithms
The pca function imposes a sign convention, forcing the element with
the largest magnitude in each column of coefs to be positive. Changing the
sign of a coefficient vector does not change its meaning.
Alternative Functionality
App
To run pca interactively in the Live Editor, use the
Reduce
Dimensionality Live Editor task.
References
[1] Jolliffe, I. T. Principal Component Analysis. 2nd ed., Springer, 2002.
[2] Krzanowski, W. J. Principles of Multivariate Analysis. Oxford University Press, 1988.
[3] Seber, G. A. F. Multivariate Observations. Wiley, 1984.
[4] Jackson, J. E. A. User's Guide to Principal Components. Wiley, 1988.
[5] Roweis, S. “EM Algorithms for PCA and SPCA.” In Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems. Vol.10 (NIPS 1997), Cambridge, MA, USA: MIT Press, 1998, pp. 626–632.
[6] Ilin, A., and T. Raiko. “Practical Approaches to Principal Component Analysis in the Presence of Missing Values.” J. Mach. Learn. Res.. Vol. 11, August 2010, pp. 1957–2000.
Extended Capabilities
This function supports tall arrays for out-of-memory data with some limitations.
pcaworks directly with tall arrays by computing the covariance matrix and using the in-memorypcacovfunction to compute the principal components.Supported syntaxes are:
coeff = pca(X)[coeff,score,latent] = pca(X)[coeff,score,latent,explained] = pca(X)[coeff,score,latent,tsquared] = pca(X)[coeff,score,latent,tsquared,explained] = pca(X)
If
Xis a tall array,coeffis ap-by-pnumeric matrix, wherep=size(X,2).Name-value pair arguments are not supported.
For more information, see Tall Arrays for Out-of-Memory Data.
Usage notes and limitations:
When
'Algorithm'is'als', the'Display'value for'Options'is ignored.The values for the
'Weights'and'VariableWeights'name-value pair arguments must be real.The value for the
'Economy'name-value pair argument must be a compile-time constant. For example, to use the'Economy',falsename-value pair argument in the generated code, include{coder.Constant('Economy'),coder.Constant(false)}in the-argsvalue ofcodegen(MATLAB Coder).Names in name-value arguments must be compile-time constants.
The generated code always returns the fifth output
explainedas a column vector.The generated code always returns the sixth output
muas a row vector.If
muis empty,pcareturnsmuas a 1-by-0 array.pcadoes not convertmuto a 0-by-0 empty array.The generated code does not treat an input matrix
Xthat has allNaNvalues as a special case. The output dimensions are commensurate with corresponding finite inputs.To save memory on the device to which you deploy generated code, you can separate training (constructing PCA components from input data) and prediction (performing PCA transformation). Construct PCA components in MATLAB®. Then, define an entry-point function that performs PCA transformation using the principal component coefficients (
coeff) and estimated means (mu), which are the outputs ofpca. Finally, generate code for the entry-point function. For an example, see Apply PCA to New Data and Generate C/C++ Code.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
Usage notes and limitations:
You cannot specify the name-value argument
Algorithmas"als".The EIG algorithm is generally faster than SVD when the number of variables is large.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2012b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)