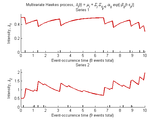
The submission considers first-order exponential-decay Hawkes processes with constant unconditional intensities, and presents
a) a calculation of point-time intensities for constituent series of a multivariate process;
b) a plotting function visualizing intensity dynamics and event occurrences of a multivariate process;
c) a *univariate* process simulator, based on Algorithm 1 of Bravaccino (2004, p. 80). A multivariate simulator is desired, and collaboration is enthusiastically welcomed.
Cite As
Dimitri Shvorob (2024). Simulate a Hawkes process (https://www.mathworks.com/matlabcentral/fileexchange/17983-simulate-a-hawkes-process), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Statistics and Machine Learning Toolbox > Descriptive Statistics and Visualization >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
hawkes/
hawkes/html/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 | BSD
|