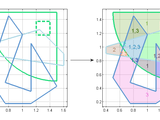
function [Geo] = Polygons_intersection(S,Display_result,Accuracy)
% This function computes n-times intersection region of shapes collection
% and allows to identify every intersection region in which shapes
% intersect.
%
% The function takes one argument as input, a structure S containing
% geometrical descriptions of shapes, and delivers one output argument,
% a structure containing the different shape intersections, with the
% shape indexes involded in the intersection and the associated area.
% The second argument is optional. Display_result is a binary value which
% indicates whether the result should be displayed (1) or not (0).
%
% Input: S : Structure containing geometrical description of polygons.
% S(i) contains all information relative to the i-th shape
% S(i).P(j) gives access to the geometrical description of the j-th
% element of the i-th shape.
% XData : S(i).P(j).x : Vector
% YData : S(i).P(j).y : Vector
% Hole : S(i).P(j).hole : Binary value (1= hole, 0= fill).
% This binary variable indicates whether the consider polygon
% S(i).P(j) is a hole or not. Hole are represented with
% dotted lines on figures.
% Display_result: Binary value used to display or not result
% Accuracy: Relative accuracy. The accuracy of the algorithm
% will the product of this parameter and the area of the largest
% polygon
%
% Output: Geo : Structure containing geometrical description of the
% intersection polygons, their area, and shape indexes used
% to compute the intersection.
%
% Geo(i).index contains the polygon indexes
% Geo(i).P contains the geometry of the polygon
% P is a structure containing XData &
% YData of polygons.
% XData : Geo(i).P(j).x : Vector
% YData : Geo(i).P(j).y : Vector
% Hole : Geo(i).P(j).hole : Binary value (1
% = hole, 0= fill)
% Geo(i).area contains the area of the i-th shape.
%
% This function starts to evaluate the intersection between all shapes.
% Results are stored in an intersection matrix M, where M(i,j) contains the
% intersection between shape i & j.
% Then, for each shape which intersects other shapes, one lists all
% possible polygons involved in the intersection with the function
% Polygons_intersection_Create_combination. The results is a list of
% possible intersection, each element of this list is tested and each time
% there is intersection, a new shape is created with the attribute of the
% polygons involved in the intersection.
%
% Then, new shapes that are the results of several intersection
% computations are substracted to polygons lower shape indexes.
%
% This function uses Polygon Clipper, a function posted by Sebastian Hlz:
%
% "The Polygon Clipper (based on the gpc-library) is used to performe
% algebraic operations on two polygons.
% Given two arbitrary polygons (which may self intersect, may contain
% holes, may be constructed of several contours) the Polygon Clipper
% is used to calculate the resulting polygon for the operations diff,
% union, AND, XOR.
%
% Credit for the gpc-library goes to Alan Murta."
%
%
%
% Guillaume JACQUENOT
% guillaume at jacquenot at gmail dot com
% 2007_10_08
% 2009_06_16
if nargin==0
% Creates initial geometry for an example.
S(1).P(1).x = [1.5 1.5 0.5 1.5+cos(pi:pi/30:3*pi/2)];
S(1).P(1).y = [0.5 1.5 1.5 1.5+sin(pi:pi/30:3*pi/2)];
S(1).P(1).hole = 0;
S(1).P(2).x = [0.7 0.9 0.9 0.7 0.7]+0.5;
S(1).P(2).y = [0.9 0.9 1.1 1.1 0.9]+0.27;
S(1).P(2).hole = 1;
S(2).P(1).x = [0.4 0.4 1.6 1.6 1.25 0.4];
S(2).P(1).y = [1 0.9 0.725 0.9 1.25 1];
S(2).P(1).hole = 0;
S(3).P(1).x = [0.5 0.75 1.125 1.5 1.125 1.125 0.75 1 0.8 0.5];
S(3).P(1).y = [0.5 0.125 0.125 0.375 1 0.3 0.43 1.125 1.4 0.5]+0.05;
S(3).P(1).hole = 0;
Display_result = 1;
Accuracy = 1e-6;
Polygons_intersection(S,Display_result,Accuracy);
clear S
S(1).P.x = [0 -10.9180 -9.8212 1.0968 0];
S(1).P.y = [0 -1.3406 -10.2735 -8.9329 0];
S(2).P.x = [6 -4.9180 -3.8212 7.0968 6];
S(2).P.y = [0 -1.3406 -10.2735 -8.9329 0];
S(3).P.x = [6 -4.9180 -3.8212 7.0968 6];
S(3).P.y = [5 3.6594 -5.2735 -3.9329 5];
S(4).P.x = [0 -10.9180 -9.8212 1.0968 0];
S(4).P.y = [5 3.6594 -5.2735 -3.9329 5];
S(1).P.hole = 0;
S(2).P.hole = 0;
S(3).P.hole = 0;
S(4).P.hole = 0;
Display_result = 1;
Accuracy = 1e-6;
Polygons_intersection(S,Display_result,Accuracy);
return;
elseif nargin == 1
Display_result = 0;
Accuracy = 1e-6;
elseif nargin == 2
Accuracy = 1e-6;
end
% Number of polygons stored in N_polygons
N_polygons = numel(S);
for i=1:N_polygons
S(i).index = i;
end
% Compute the area of all elements
S = Polygons_intersection_Compute_area(S);
% Compute total accuracy
Accuracy = Accuracy * max([S(:).area]);
% Preallocating memory to store intersection area between polygons.
Res = zeros(N_polygons);
% Initiate index, which will used to store domains
index = 1;
% Storing_index is used to know where the information of the intersection
% polygons i & j is stored in the output structure Geo
Storing_index = zeros(N_polygons);
% Performs a double sweep on all polygons to perform a first polygon
% intersection
% index is used to count the number of intersections
% Geo is used to the output structure containing all intersection results
% Compute a first level intersection
for i = 1:N_polygons-1
for j = i+1:N_polygons
P = PolygonClip(S(i).P,S(j).P,1);
% if the intersection is not empty
if size(P,2)~=0
% for all elements of P
for p = 1:size(P,2)
Res(i,j) =Res(i,j) + (1-2*P(p).hole)*polyarea(P(p).x,P(p).y);
end
Storing_index(i,j)=index;
% Initiates Geo, structure containing all results.
Geo(index).index = [i,j];
Geo(index).P = P;
Geo(index).area = Res(i,j);
index = index +1;
end
end
end
index_first = index -1;
% This function creates a list of all possible overlapping elements
% computed from an intersection area matrix
Index2 = Polygons_intersection_Create_combination(Res);
V = zeros(1,numel(Index2));
for i=1:numel(Index2)
Geo(index_first+i).index = Index2(i).data;
j=1;
str2compare = Index2(i).data(1:end-1);
N_str2compare = numel(str2compare);
bool=0;
while (j<=index_first+i-1) && bool==0
if length(str2compare)==length(Geo(j).index);
if sum(str2compare == Geo(j).index)==N_str2compare
bool=1;
else
j=j+1;
end
else
j=j+1;
end
end
V(i)=j;
end
% One computes possible polygon intersections.
To_delete = [];
for i=1:numel(Index2)
if ~isempty(Geo(V(i)).P)
P=PolygonClip(Geo(V(i)).P,S(Index2(i).data(end)).P,1);
if size(P,2)~=0
area = 0;
for p = 1:size(P,2)
area = area + (1-2*P(p).hole)*polyarea(P(p).x,P(p).y);
Geo(index_first+i).P = P;
Geo(index_first+i).area = area;
end
else
To_delete = [To_delete,index_first+i];
end
else
To_delete = [To_delete,index_first+i];
end
end
Geo(To_delete)=[];
% Posttreatment
N_Geo = numel(Geo);
for i=1:N_Geo
for j=1:numel(Geo(i).P)
% Polygons are closed
if ((Geo(i).P(j).x(end)~=Geo(i).P(j).x(1)) ||...
(Geo(i).P(j).y(end)~=Geo(i).P(j).y(1)))
Geo(i).P(j).x = [Geo(i).P(j).x;Geo(i).P(j).x(1)];
Geo(i).P(j).y = [Geo(i).P(j).y;Geo(i).P(j).y(1)];
end
end
end
% N_Geo = numel(Geo);
% colour = rand(N_Geo,3);
% figure, hold on, grid on
% for i=1:N_Geo
% for j=1:numel(Geo(i).P)
% h = plot(Geo(i).P(j).x,Geo(i).P(j).y,'color',colour(i,:),'LineWidth',3);
% if Geo(i).P(j).hole==1
% set(h,'LineStyle','--');
% end
% % text(S(n).x(1)+0.2,S(n).y(1)+0.2,num2str(n),...
% % 'color',colour(n,:),'FontSize',14);
% end
% end
% Now that the all intersection polygons have been computed, one calls the
% following function that will splits the original polygons into smaller
% ones
Geo = Polygons_intersection_Posttreatment(S,Geo,Display_result,Accuracy);
