Viewer3D
Editor's Note: Popular File 2016
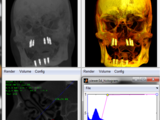
This function can be used to interactively view any kind of 2D,3D and 4D image volumes like CT and MRI. Allowing segmentation and distance measurements or ROI selection in 2D slices.
It includes Maximum intensity projections (MIP), Volume Rendering (VR) , Slice render, and colored and Phong shaded Volume rendering.
Voxel opacity and color tables can be changed on the fly allowing also iso surface kind of renders.
The fast render algorithm which renders a 3D volume to a 2D image, is based on a Matlab coded implementation of the Shear-Warp transform, in which instead of rotating the viewer rays the slices are sheared.
There are two major Matlab files:
- viewer3d.m : The interactive GUI
- render.m : The function which renders volume data with the shear-warp transform to an 2D image.
File-formats supported:
Matlab Files (.mat)
Dicom Files ( .dcm , .dicom )
V3D Philips Scanner ( .v3d )
GIPL Guys Image Processing Lab ( .gipl )
HDR/IMG Analyze ( .hdr )
ISI Files ( .isi )
NifTi ( .nii )
RAW files ( .raw , .* )
VMP BrainVoyager ( .vmp )
XIF HDllab/ATL ultrasound ( .xif )
VTK Visualization Toolkit ( .vtk )
Insight Meta-Image ( .mha, .mhd )
Micro CT ( .vff )
Note:
This version is 100% Matlab code, but to make it faster if you run "compile c-code" in the config menu. I also included an older version with the shearwarp algorithm in c-code / mex-code
Please report bugs, successes and if you know some possible code speedups.
Cite As
Dirk-Jan Kroon (2024). Viewer3D (https://www.mathworks.com/matlabcentral/fileexchange/21993-viewer3d), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Image Processing Toolbox > 3-D Volumetric Image Processing >
- Industries > Medical Devices > DICOM Format >
- MATLAB > Graphics > 2-D and 3-D Plots > Surfaces, Volumes, and Polygons > Volume Visualization > Scalar Volume Data >
- MATLAB > Graphics > Images > Read, Write, and Modify Image >
- Sciences > Physics > Medical Physics >
- Engineering > Biomedical Engineering > Biomedical Imaging >
Tags
Acknowledgements
Inspired: pcolor3, max_in_place - example of multi-threaded MEX function, Microscopy Image Browser (MIB), Microscopy Image Browser 2 (MIB2)
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Old_Viewer3D_with_c_code/
Old_Viewer3D_with_c_code/mex_c-code/
ReadData3D/
ReadData3D/dicom/
ReadData3D/gipl/
ReadData3D/hdr/
ReadData3D/isi/
ReadData3D/mha/
ReadData3D/nii/
ReadData3D/par/
ReadData3D/raw/
ReadData3D/subfunctions/
ReadData3D/v3d/
ReadData3D/vff/
ReadData3D/vmp/
ReadData3D/vtk/
ReadData3D/xif/
SubFunctions/
SubFunctions/BasicSnake_version2d/
| Version | Published | Release Notes | |
|---|---|---|---|
| 12.1.0.0 | Fixed mouse-position bug in R2015a |
||
| 12.0.0.0 | Now works with new Matlab versions such as R2015a. Thank you, "Zhensen Chen" for pointing out the UIpanel issue.
|
||
| 1.26.0.0 | Added 4D support, color overlay and many other changes. |
||
| 1.24.0.0 | Major update : Added multiple window and multiple volume support. |
||
| 1.22.0.0 | Fixed Bug number of input arguments slice view, and fixed bug in window-level slider |
||
| 1.21.0.0 | Replaced the c-code Affine Warp files. Now scaling is not longer always 0..1 but supports scales and units like Hounsfield |
||
| 1.19.0.0 | Updated File-formats |
||
| 1.18.0.0 | Fixed folder location compile_c_files, changed text in code from dicom to data3d |
||
| 1.17.0.0 | Sorted files into sub-folders, now can read many medical-formats with ReadData3D |
||
| 1.16.0.0 | Fixed Dicom Sorting problem |
||
| 1.15.0.0 | Added Dicom Info dialog.
|
||
| 1.14.0.0 | Solved major bugs in Dicom volume reading |
||
| 1.13.0.0 | Bug in "Load View" solved |
||
| 1.12.0.0 | Now read single Dicom files containing a whole 3D/4D volume.
|
||
| 1.11.0.0 | Now "Autocontrast" is automatically enabled if someone uses uint16 and the data uses only a part of the rang 0 to 2^16-1 |
||
| 1.10.0.0 | Linux Ubuntu tested |
||
| 1.9.0.0 | Removed unnecessary code from mouse position read out. Maybe this fixed the mouse position out of sync bug, which occurred sometimes. |
||
| 1.8.0.0 | Slice rendering and measurements, multi-threaded image warp code, bugs fixed. |
||
| 1.6.0.0 | Configuration screen, with trade off between quality, memory and speed. Implemented most suggestions by Cris Luengo. Some small bug fixes and optimizations. |
||
| 1.5.0.0 | Now 100% Matlab code, no mex files needed. Also warp 2D interpolation bug and save/load bug fixed. |
||
| 1.2.0.0 | fixed small dimension bug in major viewing axis. And files to folders |
||
| 1.1.0.0 | Extended the help (with pictures) and updated error check |
||
| 1.0.0.0 |