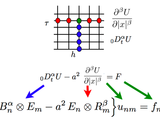
Matrix approach to discretization of ODEs and PDEs of arbitrary real order
This submission contains the basic functions that are necessary for using the matrix approach to discretization of fractional differential equations, and demos.
The method is described in the following articles:
[1] I. Podlubny, "Matrix approach to discrete fractional calculus", Fractional Calculus and Applied Analysis, vol. 3, no. 4, 2000, pp. 359-386 (http://people.tuke.sk/igor.podlubny/pspdf/ma2dfc.pdf ).
[2] I. Podlubny, A. Chechkin, T. Skovranek, YQ. Chen, B. M. Vinagre Jara, "Matrix approach to discrete fractional calculus II: partial fractional differential equations", Journal of Computational Physics, vol. 228, no. 8, 1 May 2009, pp. 3137-3153, http://dx.doi.org/10.1016/j.jcp.2009.01.014 (preprint: http://arxiv.org/abs/0811.1355 ).
For more information about fractional differential equations (i.e., differential equations containing derivatives of arbitrary real order) see, for example,
[3] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999, ISBN 0125588402.
======================
Update notes 2008-11-27:
(1) Added a tutorial article (in the form of a "published m-file") with examples. The examples include: evaluation of integer-order derivatives; evaluation of left-sided and right-sided Riemann-Liouville fractional derivatives; evaluation of symmetric fractional derivatives (symmetric Riesz derivatives); solution of a fractional integral equation with Riesz kernel; solution of an ordinary fractional differential equation (the Bagley-Torvik equation); solution of a partial fractional differential equation (fractional diffusion equation); solution of a partial fractional differential equation with delayed fractional derivatives (fractional diffusion equation with delayed fractional derivative).
(2) Added two demo functions (bagleytorvikequation.m and rieszpotential.m)
(3) Updated the title of this submission by adding the words "of arbitrary real order".
======================
Update notes 2008-12-04:
(1) Corrected typos in the description.
(2) Deleted unused files in 'html' directory.
(3) Low quality PNG images of equations in the tutorial, that were generated by Matlab when "publishing to HTML", are replaced with PNG images of good quality obtained using TeX.
======================
Update notes 2009-01-07:
Spelling corrections in the "published m-file" and in descriptions inside the functions.
======================
Update notes 2009-02-05:
Added journal reference.
======================
Update notes 2009-04-24:
Updated function fracdiffdemou.m
(thanks to Dr. Mridula Garg, University of Rajasthan)
Cite As
Igor Podlubny (2024). Matrix approach to discretization of ODEs and PDEs of arbitrary real order (https://www.mathworks.com/matlabcentral/fileexchange/22071-matrix-approach-to-discretization-of-odes-and-pdes-of-arbitrary-real-order), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Mathematics > Numerical Integration and Differential Equations > Ordinary Differential Equations >
Tags
Acknowledgements
Inspired: FracApp: numerical differ-integrals of fractional order, MCFD Toolbox
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
html/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.13.0.0 | MathWorks update: Added Live Script.
|
||
| 1.12.0.0 | Updated function fracdiffdemou.m
|
||
| 1.11.0.0 | Update the link to the preprint. |
||
| 1.10.0.0 | Updated the journal reference in the description. |
||
| 1.9.0.0 | Updated description (added journal reference). |
||
| 1.8.0.0 | Deleted an unused file. |
||
| 1.7.0.0 | Spelling corrections in the "published m-file" and in descriptions inside the functions. |
||
| 1.6.0.0 | (1) Corrected typos in the description. (2) Deleted unused files in 'html' directory. (3) Low quality PNG images of equations generated by Matlab are replaced with better ones. |
||
| 1.5.0.0 | (1) Added a tutorial ("published m-file") with examples. For details see the description of this submission. (2) Added two demo functions. (3) Updated the title of this submission by adding the words "of arbitrary real order". |
||
| 1.4.0.0 | Updated ZIP file structure. |
||
| 1.3.0.0 | Updated ZIP file structure. |
||
| 1.2.0.0 | Updated ZIP file structure. |
||
| 1.1.0.0 | Updated ZIP file structure. |
||
| 1.0.0.0 |