TRIGDEMO
Editor's Note: This file was selected as MATLAB Central Pick of the Week
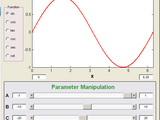
Interactively explore how parameters affect trigonometric functions. TRIGDEMO allows user to manipulate the parameters A,B,C,D in the general equation:
y = y(x) = A trig(Bx + C) +D
Where trig is any one of sine, cosine, tangent, cosecant, secant, cotangent.
The inspiration for this was my participation in a discussion, during the course of which, it became clear that several very educated people didn't completely (reflexively) understand how these parameters affect the plot of trigonometric functions.
I figure if these folks were hesitant, there might be others out there who could use a little refresher.
For demonstration purposes only! This is not meant to be earth-shattering.
Cite As
Matt Fig (2024). TRIGDEMO (https://www.mathworks.com/matlabcentral/fileexchange/22664-trigdemo), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Graphics > 2-D and 3-D Plots > Line Plots > Change Markers >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |