MPC Tutorial III: MPC in Simulink V2
Based on the state space MPC code in File Exchange, http://www.mathworks.com/matlabcentral/fileexchange/19650
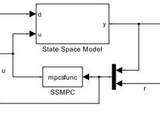
a Simulink block to use the state space MPC code is developed. Two examples to work with continous-time state space plant model and discrete-time state space plant model are included.
Cite As
Yi Cao (2024). MPC Tutorial III: MPC in Simulink V2 (https://www.mathworks.com/matlabcentral/fileexchange/22790-mpc-tutorial-iii-mpc-in-simulink-v2), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: MPC Tutorial II: Multivariable and State Space MPC V2.0
Inspired: MPC Tutorial IV - State Space MPC with input increment
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.