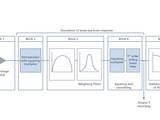
Flickermeter Simulator
Cite As
Patrik Jourdan (2024). Flickermeter Simulator (https://www.mathworks.com/matlabcentral/fileexchange/24423-flickermeter-simulator), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: Light flicker assessment toolbox
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
flicker_sim
| Version | Published | Release Notes | |
|---|---|---|---|
| 2.3.0.0 | Minor correction according to Corrigendum 1 of IEC 61000-4-15 edition 2.0 2010-08.
|
||
| 2.2.0.1 | Corrected comment in example_testbench_50Hz.m according to feedback from Søren Vejlgaard Vedstesen |
||
| 2.2.0.0 | Improved numerical stability |
||
| 2.1.0.0 | Minor bug fix in coefficient of weighting filter for 120V system.
|
||
| 2.0.0.0 | updated simulator to IEC 61000-4-15 Edition 2.0
|
||
| 1.6.0.0 | updated URL in description and file comments |
||
| 1.5.0.0 | updated URL in description |
||
| 1.4.0.0 | minor bug fix in flicker_sim: fixed typo in computation of p_50s
|
||
| 1.2.0.0 | minor bug fix in power_to_line_voltage: missing scaling factor sqrt(2) (reported by: Kjar Soren Bakhoj) |
||
| 1.1.0.0 | Added description of package contents and updated code comments |
||
| 1.0.0.0 |