SLM - Shape Language Modeling
If you could only download one curve fitting tool to your laptop on a desert island, this should be it.
For many years I have recommended that people use least squares splines for their curve fits, with a caveat. Splines offer tremendous flexibility to build a curve in any shape or form. They can nicely fit almost any set of data you will throw at them. This same flexibility is their downfall at times too. Like polynomial models, splines can be too flexible if you are not careful. The trick is to bring your knowledge of the system under study to the problem.
As a scientist, engineer, data analyst, etc., you often have knowledge of a process that you wish to model. Sometimes that knowledge comes from physical principles, sometimes it arises from experience, and sometimes the knowledge just comes from looking at a plot of the data. Regardless of the source, we often want to build in this prior knowledge of a process into our modeling efforts. This is perhaps the biggest reason why nonlinear regression tools are used, and I'll argue, the worst reason. If you are fitting a sigmoid function to your data only because it happens to be monotone and your data appear to have that property, then you have made the wrong choice of modeling tool. (If you are fitting a sigmoid because this is known to be the proper model for your process, then go ahead and fit the sigmoid.)
I'll argue the proper tool when you merely need a monotonic curve fit is a least squares spline, but a spline that is properly constrained to have the fundamental shape you know to be there. This is a very Bayesian approach to modeling, and a very useful one in my experience.
The SLM tools provided here give you an easy to use interface to build an infinite number of curve types from data. SLM stands for Shape Language Modeling. The idea is to provide a prescription for a curve fit using a set of shape primitives. If your curve is monotone, then build that information into the model, so you can estimate the monotone curve that best fits your data. What you will find is that once you employ the proper set of constraints, you will wonder why you ever used nonlinear regression in the past!!!
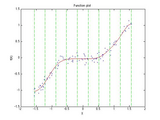
For example, the screenshot for this file was generated for the following data:
x = (sort(rand(1,100)) - 0.5)*pi;
y = sin(x).^5 + randn(size(x))/10;
slm = slmengine(x,y,'plot','on','knots',10,'increasing','on', ...
'leftslope',0,'rightslope',0)
slm =
form: 'slm'
degree: 3
knots: [10x1 double]
coef: [10x2 double]
prescription: [1x1 struct]
x: [100x1 double]
y: [100x1 double]
You can evaluate the spline or its derivatives using slmeval.
slmeval(1.3,slm)
ans =
0.79491
You plot these splines using plotslm.
plotslm(slm)
The plotslm function is nice because it is a simple gui, allowing you to plot the curve, residuals, its derivatives or the integral. You can also evaluate various parameters of the spline, such as the maximum function value over an interval, the minimum or maximum slope, etc.
slmpar(slm,'maxslope')
ans =
1.5481
You provide all this information to slmengine using a property/value pair interface. slmset mediates this interaction, so you can use it to create the set of properties that will be used. The default set of properties and their values are given by slmset. Everything about the shape, slopes, curvature, values, etc., about your function can be controlled by a simple command. SLMENGINE also offers the ability to generate splines of various orders, as well as free knot splines.
For a complete set of examples of the SLM tools in action, see the included published tutorial with this submission. There is also a small treatise included on the concept of Shape Language Modeling for curve fitting.
The SLM toolkit will be considerably improved at some time in the future. I will add a graphical interface. As well, if I have missed any natural shape primitives, please let me know. While I have tried to be very inclusive, surely there is something I've missed. If I can add your favorite to the list above I will try to do so.
Finally, the SLM tools require the optimization toolbox to solve the various estimation problems.
Cite As
John D'Errico (2026). SLM - Shape Language Modeling (https://www.mathworks.com/matlabcentral/fileexchange/24443-slm-shape-language-modeling), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI and Statistics > Curve Fitting Toolbox > Linear and Nonlinear Regression >
- AI and Statistics > Curve Fitting Toolbox > Splines >
- Computational Finance > Financial Instruments Toolbox > Price Instruments Using Functions > Yield Curves >
- AI and Statistics > Statistics and Machine Learning Toolbox > Descriptive Statistics and Visualization > Statistical Visualization > Box Plots >
Tags
Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.