DFiltFIR
DFiltFIR designs linear phase Finite (length) Impulse Response (FIR) filters. It can be considered to extend the functionality of the Matlab routine firpm.
DFiltFIR is a fully Matlab implementation. It started as a Fortran program based on the original McClellan-Parks code in [1]. The Fortran code was later modified to include constraints as described by Grenez [2]. At each stage of modification, more comments were added to help in understanding the code. The Fortran code was converted to the C-language and modularized allowing it to be called from programs which designed Nyquist filter and Minimum Phase filters. Finally, when desktop computation power had crossed an appropriate threshold, the program was converted into Matlab. The Matlab code is much easier to maintain and much easier to understand.
Features:
1. Each of the bands in the filter specifications is defined as a sequence of frequencies. At a minimum, bands of non-zero extent are defined by the end points of a band. Additional points within the band can be specified. The desired values, weights, and limits can be defined at those points. The design procedure interpolates these values, weights and limits onto a dense grid of frequency points.
2. The interpolation uses a monotonic cubic interpolation (similar to the Matlab routine pchip). Such an interpolation is applied segment by segment within a band and ensures that the interpolated values between the given frequency points are monotonic.
3. The dense grid of points has a density which varies within a band – the density is higher at the edges of a band than in the middle. The dense grid is applied separately between points within a band, i.e. the points in the band will appear as part of the dense grid.
4. Several versions of the interpolation are available. A function is used to transform the values to be interpolated, interpolation is applied, and then the inverse function is applied. The functions available are the identity function, log, and square root. The first is the default. The second allows for cubic interpolation of dB values of the desired values. The square root option is useful for designing minimum-phase filters (see the DFiltMPFIR package which calls the present package).
5. Relative to firpm, this program features the following.
a. More flexible definition of values, weights.
b. Band values are subject to limits.
Example Design:
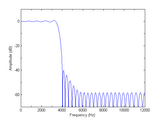
The following design is a low pass filter (127 coefficients) with two bands: a passband from 0 to 3450 Hz, and a stopband from 4000 to 24000 Hz. The sampling frequency is 48000 Hz. The desired value in the passband is 1 and the desired value in the stopband is 0. The weight in the passband varies from 5 down to 1. This means that the passband ripple amplitude at near zero frequency is 1/5 of the ripple at the passband edge. The weights for the stopband are given in two segments. The limits on the passband are such that at zero frequency, the response is forced to be unity (the upper and lower limits are both 1 at that point). By setting the upper limit to infinity and the lower limit to minus infinity, there are effectively no limits at other frequencies.
Fs = 24000;
[B(1:2).Freq] = deal([0 3450], [4000, 6000, 12000]);
[B(1:2).Value] = deal(1, 0);
[B(1:2).Weight] = deal([5 1], [10 100 100]);
B(1).LLimit = [1 -Inf];
B(1).ULimit = [1 Inf];
B(2).WeightInt = 'log';
h = DFiltFIR(63, B, 'bpf', Fs);
1. J. H. McClellan, T. W. Parks and L. R. Rabiner, “A Computer Program for Designing Optimum FIR Linear Phase Digital Filters”, IEEE Trans. Audio and Electroacoustics, vol. 21, pp. 506–526, December 1973.
2. F. Grenez, “Design of Linear or Minimum-Phase FIR Filters by Constrained Chebyshev Approximation”, Signal Processing, vol. 5, pp. 325–332, July 1983.
Cite As
Peter Kabal (2024). DFiltFIR (https://www.mathworks.com/matlabcentral/fileexchange/24662-dfiltfir), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > Signal Processing Toolbox > Digital and Analog Filters > Digital Filter Design > FIR Filter Design >
Tags
Communities
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
DFiltFIR/
DFiltFIR/private/
DFiltFIR/private/test/
DFiltFIR/test/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |