GODLIKE - A robust single-& multi-objective optimizer
GODLIKE (Global Optimum Determination by Linking and Interchanging Kindred Evaluators) is a generization of various population-based global optimization schemes. Also, it handles both single- and multi-objective optimization, simply by adding additional objective functions.
GODLIKE solves optimization problems using relatively basic implementations of a genetic algorithm, differential evolution, particle swarm optimization and adaptive simulated annealing algorithms. Its power comes from the fact that these different algorithms run simultaneously (linked), and members from each population are occasionally swapped (interchanged) to decrease the chances of convergence to a local minimizer.
It is primarily intended to increase ROBUSTNESS, not efficiency as it usually requires more function evaluations than any of the algorithms separately. Its also inteded to do away with the need to fine-tune these algorithms each and every time you encounter an optimization problem, AND to generalize optimization itself (it's both a single and multi-objective optimizer), AND to generate simple plots to be used in quick reports etc.
BASIC EXAMPLES:
(single-objective)
% extended Rosenbrock function
rosen = @(X) sum( 100*(X(:, 2:2:end) - X(:, 1:2:end-1).^2).^2 + (1 - X(:, 1:2:end-1)).^2, 2);
% call GODLIKE
GODLIKE(rosen, -10*ones(1,10), 10*ones(1,10), 'ms')
will produce a reasonably accurate approximation to the global minimum of the 10-dimensional Rosenbrock problem
( sol ~ ([1,1,1,...]), fval ~ 0 )
(multi-objective optimization)
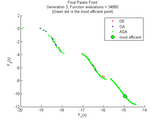
% basic Sin-Cos Pareto front
GODLIKE({@sin;@cos}, 0, 2*pi, [], 'display', 'plot')
will generate a nice plot of the problem's Pareto front. Some more examples are included in the GODLIKE_DEMO.m, included in the submission.
======================================
MAJOR CHANGES
(see the changelog for more detailed changes)
======================================
(2016/October/24)
- Moved 'popsize' and 'which_ones' from the function signature to a more intuitive place -- the options
- Improved plotting routines ('display', 'plot')
- Started major overhaul of the code base to make it easier for me to maintain and extend upon
(06/Aug/2009)
- Objective functions can now accept any 2-dimensional input. Your objective function should accept arguments equal in size to either [lb] or [ub], and return a simple scalar.
- I discovered I made some *severe* mistakes in the implementation of the global optimization algorithms. This caused large inefficiencies or inaccurate results. Most (hopefully all) of these mistakes are corrected now.
- Added 2more options for the algorithms: NetWorkTopology & ReHeat (see doc)
- Changed the [MinDescent] criterion to the more MATLAB-style 'TolX' and 'TolFun' options
Cite As
Rody Oldenhuis (2026). GODLIKE - A robust single-& multi-objective optimizer (https://github.com/rodyo/FEX-GODLIKE/releases/tag/v1.5), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Computational Finance > Econometrics Toolbox >
- Mathematics and Optimization > Optimization Toolbox > Nonlinear Optimization >
- Mathematics and Optimization > Global Optimization Toolbox > Simulated Annealing >
- Mathematics and Optimization > Global Optimization Toolbox > Multiobjective Optimization >
Tags
Acknowledgements
Inspired by: NSGA - II: A multi-objective optimization algorithm
Inspired: Simple Example of Multiobjective Evolutionary Algorithm, cengique/pandora-matlab, godlikegui
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
@objFunction
@popMulti
@popSingle
private
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.5 | See release notes for this release on GitHub: https://github.com/rodyo/FEX-GODLIKE/releases/tag/v1.5 |
||
| 1.4.0.0 | (linked to GitHub) |
|
|
| 1.2.0.0 | [linked to Github] |
|
|
| 1.1.0.0 | Lots of changes (too much to list here). See the changelog.txt file in the ZIP. |
||
| 1.0.0.0 |