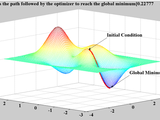
Derivative-based Optimization
This folder contains a word document (optimization_problem_wth_solution.doc) that contains a description for an optimization problem along with its solution. The folder contains two m-script file that contain the solution for the Gradient_Descent_minimum and Gradient_Descent_maximum problems included in the word document. The algorithm for the gradient descent is included in the m-script files. For more information, you could go to wikipedia.
You don't need the optimization toolbox to run the script.
Cite As
Nassim Khaled (2026). Derivative-based Optimization (https://www.mathworks.com/matlabcentral/fileexchange/27631-derivative-based-optimization), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |