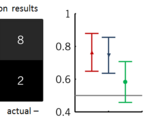
Computing the posterior balanced accuracy
In binary classification, the average accuracy obtained on individual cross-validation folds is a problematic measure of generalization performance. First, it makes statistical inference difficult. Second, it leads to an optimistic estimate when a biased classifier is tested on an imbalanced dataset. Both problems can be overcome by replacing the conventional point estimate of accuracy by an estimate of the posterior distribution of the balanced accuracy.
This archive contains a set of MATLAB functions to estimate the posterior distribution of the balanced accuracy and compute its associated statistics.
For full details, see:
K.H. Brodersen, C.S. Ong, K.E. Stephan, J.M. Buhmann (2010)
The balanced accuracy and its posterior distribution.
Proceedings of the 20th International Conference on Pattern Recognition, 3121-3124.
Cite As
Kay H. Brodersen (2024). Computing the posterior balanced accuracy (https://www.mathworks.com/matlabcentral/fileexchange/29244-computing-the-posterior-balanced-accuracy), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
PosteriorBalancedAccuracy-1.05/examples/
PosteriorBalancedAccuracy-1.05/matlab/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |