Rsyso
Version 1.0.0.0 (377 KB) by
Franklin Pineda
Finds realizations of SISO linear systems. Autonoma of Colombia University.
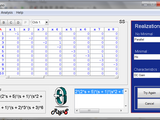
Rsyso is a user interface created with Matlab ® to facilitate management control of monovariable linear models. Among the main functions that currently presents:
• Find minimum realizations by different methods.
• Conversions and main characteristics of the SISO model (transfer functions (TF) and the state space (ss)).
• Allows transformation similarity to achievements in canonical form.
Cite As
Franklin Pineda (2024). Rsyso (https://www.mathworks.com/matlabcentral/fileexchange/30890-rsyso), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2009b
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
Find more on Robust Control Toolbox in Help Center and MATLAB Answers
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Rsyso/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |