Fit GLM with quadratic penalty
Generalized linear models (GLMs) are a natural extension of linear regression models in which eta = X*w is related to y by a fixed nonlinearity and a possibly non-Gaussian noise source. Standard linear regression, logistic regression and Poisson regression are all special types of GLMs.
This package fits GLMs with quadratic penalties. That is, if the negative log likelihood of the data with respoect to the model parameters is given by -log(p(y|w)), then glmfitqp solves the problem:
min_w (-log(p(y|w)) + .5*w'*qf'w)
This form of penalty naturally arises by assuming a prior on w, p(w) = N(0,qf^-1). Quadratic penalties can be used to impose that the weights are small (qf = lambda*I) or that the weights are smooth (qf = lambda*D).
In general qf is only known up to a multiplicative constant lambda that determines the strength of the regularization and must be determined empirically. The function cvglmfitqp finds this optimal lambda through k-fold cross-validation. The cross-validation can be parallelized through parfor (requires parallel computing toolbox).
It is also possible to consider a more general prior of the form:
-log p(w) = .5*w'*(qf0 + sum_i lambda(i) qfs(:,:,i) )
In this case evidenceglmfitqp can be used to determine the optimal set of lambdas through evidence (marginal likelihood) maximization.
Example use:
---
%%
%Figure out optimal strength of prior through cross validation
%Assume smoothness of the model parameters
qf = blkdiag(qfsmooth1D(16),.01);
rg = (-7.5:7.5)';
%Simulate a model with w = Gabor function
w = exp(-rg.^2/3^2).*sin(rg*2*pi/6);
nobs = 150;
X = [randn(nobs,length(w)),ones(nobs,1)];
r = 3*X*[w;.01];
%output is binary -> logistic regression
r = binornd(1,1./(1+exp(-r)));
%Set up 5-fold CV
folds = getcvfolds(length(r),5,1001);
%Fit the data
clear opts
opts.family = 'binomlogit';
opts.lambda0 = 1;
results = cvglmfitqp(r,X,qf,folds,opts);
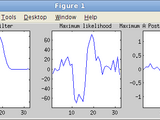
plot(results.w(1:end-1))
Cite As
Patrick Mineault (2024). Fit GLM with quadratic penalty (https://www.mathworks.com/matlabcentral/fileexchange/31661-fit-glm-with-quadratic-penalty), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.4.0.0 | Support for evidence-based optimization of hyperparameters |
||
| 1.3.0.0 | Support for Hessian-based optimization, weighted data points, enhanced cross-validation proposals |
||
| 1.2.0.0 | parfor supported during cross-validation, better scheme for determining initial lambda |
||
| 1.1.0.0 | Bug fixes and more sophisticated cvglmfitqp |
||
| 1.0.0.0 |