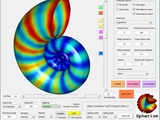
Spherium
Spherium allows for the creation of a cornicopia of curious 3D objects and offers full interactive control over lighting and orientation.
Spherium also allows for Hydrogenic orbitals to be visualized, all the way up to H I6 !
Any JPEG can be texture mapped onto the spherical object, which is defined in terms of functions of elevation (elev) and azimuth (azi). The same idea is used to define the transparency of the object.
Cite As
Andrew French (2024). Spherium (https://www.mathworks.com/matlabcentral/fileexchange/32084-spherium), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Graphics > Formatting and Annotation > 3-D Scene Control > Lighting, Transparency, and Shading >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.