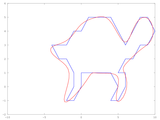
Elliptic fourier for shape analysis
1) plot_chain_code(ai, color, line_width)
This function will plot the given chain code. The chain code (ai) should be in
column vector.
Example:
>> ai = [5 4 1 2 3 4 3 0 0 1 0 1 0 0 0 7 7 1 1 0 7 5 4 5 4 5 0 6 5 4 1 3 4 4 4 4 6];
>> plot_chain_code(ai)
2) plot_fourier_approx(ai, n, m, normalized, color, line_width)
This function will plot the Fourier approximation, given a chain code (ai),
number of harmonic elements (n), and number of points for reconstruction (m).
Normalization can be applied by setting "normalized = 1".
3) output = calc_traversal_dist(ai, n, m, normalized)
This function will generate position coordinates of chain code (ai). Number of
harmonic elements (n), and number of points for reconstruction (m) must be
specified.
The output is a matrix of [x1, y1; x2, y2; ...; xm, ym].
3) output = fourier_approx(ai, n, m, normalized)
This function will generate position coordinates of Fourier approximation of
chain code (ai). Number of harmonic elements (n), and number of points for
reconstruction (m) must be specified.
The output is a matrix of [x1, y1; x2, y2; ...; xm, ym].
4) output = calc_harmonic_coefficients(ai, n)
This function will calculate the n-th set of four harmonic coefficients.
The output is [an bn cn dn]
5) [A0, C0] = calc_dc_components(ai)
This function will calculate the bias coefficients A0 and C0.
6) output = calc_traversal_dist(ai)
Traversal distance is defined as accumulated distance travelled by every
component of the chain code assuming [0 0] is the starting position.
Example:
>> x = calc_traversal_dist([1 2 3])
x =
1 1
1 2
0 3
7) output = calc_traversal_time(ai)
Traversal time is defined as accumulated time consumed by every
component of the chain code.
Example:
>> x = calc_traversal_time([1 2 3])
x =
1.4142
2.4142
3.8284
Cite As
Auralius Manurung (2024). Elliptic fourier for shape analysis (https://www.mathworks.com/matlabcentral/fileexchange/32800-elliptic-fourier-for-shape-analysis), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Image Processing Toolbox > Image Segmentation and Analysis > Image Transforms >
Tags
Acknowledgements
Inspired by: Elliptical Fourier shape descriptors
Communities
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.