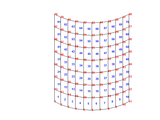
Meshing thin shells using four noded elements
To discretize thin shells using four noded elements. Thin cylindrical shells, spherical shells and conical shells can be meshed/discretized using four and three noded elements to use in Finite Element Analysis. On entering necessary inputs like length, breadth, radius, angle, number of elements etc., a Finite Element Mesh is plotted and nodal connectivity's and nodal coordinates are obtained.
For further updates, documentation check my homepage link:
https://sites.google.com/site/kolukulasivasrinivas/
Cite As
KSSV (2024). Meshing thin shells using four noded elements (https://www.mathworks.com/matlabcentral/fileexchange/34143-meshing-thin-shells-using-four-noded-elements), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Partial Differential Equation Toolbox > Domain-Specific Modeling > Structural Mechanics >
Tags
Acknowledgements
Inspired by: Meshing a plate using four noded elements
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Shell Mesh/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |