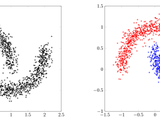
Fast and efficient spectral clustering
SpectralClustering performs one of three spectral clustering algorithms (Unnormalized, Shi & Malik, Jordan & Weiss) on a given adjacency matrix. SimGraph creates such a matrix out of a given set of data and a given distance function.
==================================
UPDATE 09/13/2012
This major update to the final version includes
[+] Full GUI
[+] Several Plot Options: 2D/3D, Star Coordinates, Matrix Plot
[+] Save Plots
[+] Save and Load all kind of data (pure data, similarity graph, clustered data)
[+] Differentiates between already labeled and unlabeled data (see README).
==================================
The code has been optimized (within Matlab) to be both fast and memory efficient. Please look into the files and the Readme.txt for further information.
References:
- Ulrike von Luxburg, "A Tutorial on Spectral Clustering", Statistics and Computing 17 (4), 2007
If there are any questions or suggestions, I will gladly help out. Just contact me at admin (at) airblader (dot) de
Cite As
Ingo (2026). Fast and efficient spectral clustering (https://www.mathworks.com/matlabcentral/fileexchange/34412-fast-and-efficient-spectral-clustering), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: relativepath.m, export_fig
Inspired: Variational Bayesian Mixture of Probabilistic PCA for Shapes
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
ImageSegmentation/
datasets/rainbowdash/
files/
files/GUI/
files/GUI/funcs/
files/GUI/funcs/getFuncs/
files/GUI/funcs/plotFuncs/
files/GUI/funcs/setFuncs/
files/GUI/funcs/toggleFuncs/
files/SimilarityGraph/
files/other/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.10.0.0 | Final update including full GUI and more. See description for details. |
||
| 1.8.0.0 | Included acknowledgements |
||
| 1.7.0.0 | - Fixed critical mistake when creating similarity graphs - Restructured some of the code |
||
| 1.6.0.0 | Fixed critical bug when creating sparse matrices Demo now plots similarity graph (only use for few data points!) Minor changes |
||
| 1.5.0.0 | fixed wrong code in demo file |
||
| 1.4.0.0 | Got rid of redundant code |
||
| 1.3.0.0 | Minor updates |
||
| 1.1.0.0 | - Updated some files
|
||
| 1.0.0.0 |