Optimal Component Selection Using the Mixed-Integer Genetic Algorithm
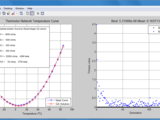
Designs often require that components come from a list of available sizes. In this example, we show how the Genetic Algorithm can be used to find values for the Resistors and Thermistors in a circuit that meet our design criteria. The example uses optimization techniques to minimize the difference between a desired response curve and the curve generated from a simulation of the circuit. Because Resistors and Thermistors are only available in standard sizes, this becomes an interger-constrained problem as our design variables are limited to these standard sizes.
Cite As
Seth DeLand (2026). Optimal Component Selection Using the Mixed-Integer Genetic Algorithm (https://www.mathworks.com/matlabcentral/fileexchange/35810-optimal-component-selection-using-the-mixed-integer-genetic-algorithm), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Optimization Toolbox > Linear Programming and Mixed-Integer Linear Programming >
- Mathematics and Optimization > Global Optimization Toolbox > Genetic Algorithm >
- Sciences > Agriculture >
Tags
Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.