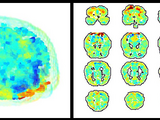
2d and 3d brain plots
Industry standard brain plotting programs are great for producing publication-quality images of brain data. However, these tools are often very slow. This suite of tools provides a means of quickly generating 2- or 3-dimensional plots of fMRI data that can be manipulated (e.g. rotated, modified) in real time.
Although these tools may be used to produce publication-quality figures, the focus here is on speed and ease of use. These tools are intended to be used for quickly exploring and examining fMRI data, debugging fMRI analyses, etc.
Note: this version is no longer maintained. Instead see: https://github.com/ContextLab/brain-plots
Cite As
Jeremy Manning (2024). 2d and 3d brain plots (https://www.mathworks.com/matlabcentral/fileexchange/36139-2d-and-3d-brain-plots), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Sciences > Neuroscience > Human Brain Mapping > MRI >
Tags
Acknowledgements
Inspired by: Plot a 3D array using patch, getTightSubplotHandles, slices, sanePColor(varargin)
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
plot_brains/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.6.0.0 | I've added two missing files and have included minor updates to several functions.
|
||
| 1.5.0.0 | Fixed some documentation errors, added support for more formats. |
||
| 1.4.0.0 | I have made a number of changes with this update that are intended to make the plotting functions easier to use. |
||
| 1.3.0.0 | added two new functions that plot from 3d matrices (tensors) rather than requiring the meta matrix. |
||
| 1.2.0.0 | Include file dependencies in the download. |
||
| 1.1.0.0 | updated documentation in plot_brain3d -- erode_layers parameter was incorrectly described in previous version. |
||
| 1.0.0.0 |