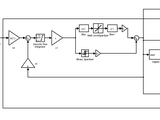
Sigma Delta Test Bench
Version 1.0.0.0 (1.43 MB) by
Aravind VJ
A test bench to simulate and analyse Sigma Delta modulators
A MATLAB + SIMULINK test bench to simulate and analyse Sigma Delta modulators. Matlab script utilises Richard Schriers Sigma Delta Toolbox and Simulink models receives modulator coefficients from the toolbox and performs various simulations.
Cite As
Aravind VJ (2024). Sigma Delta Test Bench (https://www.mathworks.com/matlabcentral/fileexchange/37822-sigma-delta-test-bench), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2011a
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
- Physical Modeling > Simscape Electrical > Electrical Block Libraries > Semiconductors and Converters >
Find more on Semiconductors and Converters in Help Center and MATLAB Answers
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
ADC_Package_Final_Submit/
ADC_Package_Final_Submit/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |