CELP codec
Version 1.0.0.0 (373 KB) by
Sourav Mondal
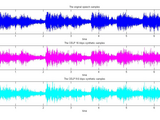
This is a code to demonstrate CELP codecs of bitrate 9.6kbps and 16kbps.
Run only the "CELP_RUN" file.
Cite As
Sourav Mondal (2024). CELP codec (https://www.mathworks.com/matlabcentral/fileexchange/39038-celp-codec), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2011b
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Data Import and Analysis > Data Import and Export > Standard File Formats > Audio and Video Data >
Find more on Audio and Video Data in Help Center and MATLAB Answers
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
CELP_done/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |