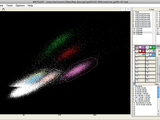
MatClust
GUI program that runs in Matlab and allows the user to draw polygons or boxes around multidimensional data points. This 'clustering' of data is used often for multi-electrode recordings of neural data. The program has been tested on Windows, Linux, and Mac platforms.
Features:
-Manual 2D clustering with polygons
-Interface for custom semi-automated sorting code
-3D rotation of feature space
-Filtering of points to precisely define each polygon’s scope
-Easy to use interface (context menus, undo states, zooming and panning)
Requires a mex compiler (free) for setup. If you don't have one, see here for easy instructions:
http://www.mathworks.com/support/compilers/R2012b/win64.html
Also, please view readme.txt for setup instructions
Cite As
Mattias Karlsson (2024). MatClust (https://www.mathworks.com/matlabcentral/fileexchange/39663-matclust), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Deep Learning Toolbox > Function Approximation, Clustering, and Control >
- Sciences > Neuroscience > Cellular Neuroscience > Electrophysiology >
- MATLAB > Language Fundamentals > Matrices and Arrays > Shifting and Sorting Matrices >
Tags
Acknowledgements
Inspired by: DecimatePoly
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
matclust_v1.4/
matclust_v1.4/ClustTools/
matclust_v1.4/Filters/
matclust_v1.4/ParameterPrograms/
matclust_v1.4/PolygonFilters/
matclust_v1.4/Tools/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.7.0.0 | Removed the object focus reset when cursor moves over cluster screen. |
||
| 1.5.0.0 | More copy-paste features/bug fixes |
||
| 1.4.0.0 | -Included 'Decimate polygon' code to reduce complexity of magic wand output
|
||
| 1.2.0.0 | Magic wand tool
|
||
| 1.1.0.0 | Version 1.4
|
||
| 1.0.0.0 |