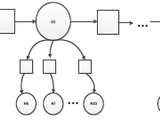
Hierarchical Kalman Filter for clinical time series prediction
It is an implementation of hierarchical (a.k.a. multi-scale) Kalman filter using belief propagation. The model parameters are estimated by expectation maximization (EM) algorithm. In this implementation, we considered two time series with different frequencies. The messages between high and low frequency signals are combined to improve the estimation and prediction.
Cite As
Shuang Wang (2024). Hierarchical Kalman Filter for clinical time series prediction (https://www.mathworks.com/matlabcentral/fileexchange/39707-hierarchical-kalman-filter-for-clinical-time-series-prediction), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
multiScale_KalmanFilter/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |