Inverse Percentiles of a sample.
USAGE
p = INVPRCTILE(x,xq)
p = INVPRCTILE(x,xq,dim)
p = INVPRCTILE(x,xq,dim,plot_pos)
INPUT:
x - Vector or Matrix of sample data
q - Values for non-exceedance probabilities to be computed.
q can be scalar or vector
dim - Dimension for matrix to be worked for non-exceedance probability
plot_pos - plotting positions that determine interpolation method
OUTPUT:
p - Non-exceedance probabilities values for q.
When x is a vector, p is the same size as xq, and p(i) contains the non-exceedance probability for xq(i) value.
When x is a matrix, the i-th row of p contains
the non-exceedance probability for xq(i)-values of each column of x.
For N-D arrays, INVPRCTILE operates along the first non-singleton dimension.
EXAMPLES:
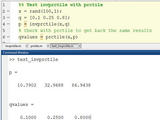
x = rand(100,1);
q = [0.1 0.25 0.8];
p = invprctile(x,q);
% Check with prctile to get back the same results
qvalues = prctile(x,p)
Cite As
Durga Lal Shrestha (2024). Inverse Percentiles of a sample. (https://www.mathworks.com/matlabcentral/fileexchange/41131-inverse-percentiles-of-a-sample), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Statistics and Machine Learning Toolbox > Descriptive Statistics and Visualization > Descriptive Statistics >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.