ProcessNetwork/ProcessNetwork_Software
Attribution
The ProcessNetwork software was written between 2005 and 2008 at the University of Illinois at Urbana-Champaign, in the Department of Civil Engineering, funded 2006-2008 by a NASA fellowship #NNX06AF71H , and then continued development has occurred at Arizona State University, funded 2013-2015 by a grant from the NSF’s Macrosystems Biology program BIO-1241960. Dr. Benjamin L. Ruddell is the primary author of the software, but many collaborators have contributed to its ongoing development. The work is that of the author, and its accuracy and implications are not necessarily supported by the funding and employing organizations. Those using the software are requested to cite the software using the following three citations, and to communicate with the author regarding modifications, extensions, and applications of the software.
Current Citation for the software:
Ruddell, B.L., C. Sturtevant, M. Kang, and R. Yu (2008), ProcessNetwork Software, version 1.5, accessed at (INSERT URL OR SOURCE HERE) on (INSERT DATE HERE).
Citations for the methods employed in the software:
Ruddell, B. L.*, and P. Kumar (2009a), Ecohydrologic process networks: 1. Identification, Water Resour. Res., 45, W03419, doi:10.1029/2008WR007279.
Ruddell, B. L.*, and P. Kumar (2009b), Ecohydrologic process networks: 2. Analysis and characterization, Water Resour. Res., 45, W03420, doi:10.1029/2008WR007280.
Ruddell, B.L.*, N. Oberg, P. Kumar, and M. Garcia (2010), Using Information-Theoretic Statistics in MATLAB to Understand How Ecosystems Affect Regional Climates, MATLAB Digest Academic Edition, February 2010, www.mathworks.com/academia.
Sturtevant, C., et al. (2015), Identifying scale-emergent, non-linear, asynchronous processes of wetland methane exchange, Journal of Geophysical Research.
Acknowledgements:
Dr. Praveen Kumar, for advising and co-authorship of publications at the University of Illinois
Dr. Ricky Robertson, for important histogram algorithm advice at the University of Illinois
Numerous students and colleagues who provided help with MATLAB coding
Cove Sturtevant and Dennis Baldocchi of the University of California, Berkeley for redevelopment of the MATLAB code in Version 1.5 to improve the processing speed of individual functions and add a wavelet transformation module, IAAFT surrogate data generation, and plotting functions.
Minseok Kang and Rong Yu for contributions to code versions 1.2 through 1.4
Introduction
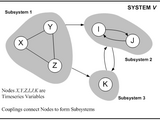
The purpose of this software is to delineate Dynamical Process Networks based on observations of information flow between discrete vector variables using information theory, including the Transfer Entropy statistic. The software also computes Shannon Entropy, Mutual Information, Relative Entropy, and many other information theoretic statistics. The software is valid for all kinds of data, but the typical application is to Dynamical information flow and Shannon Entropy, and the typical dataset a multivariate timeseries. The software is written for the MATLAB® scientific computing environment. This basic version of the software does not contain any GUI features and there are limited plotting scripts, but more of these features may be available separately. The basic version of the software contains a small set of preprocessing functions and filters, but others may also be useful.
Cite As
Ben Ruddell (2024). ProcessNetwork/ProcessNetwork_Software (https://github.com/ProcessNetwork/ProcessNetwork_Software), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
ChaosInputData
ToyInputData
wmtsa-matlab-0.2.6/munit/Examples
wmtsa-matlab-0.2.6/munit/Tests/munit
wmtsa-matlab-0.2.6/munit/munit
wmtsa-matlab-0.2.6/wmtsa
wmtsa-matlab-0.2.6/wmtsa/Examples/WMTSA_Book/Figures
wmtsa-matlab-0.2.6/wmtsa/Tests
wmtsa-matlab-0.2.6/wmtsa/Tests/data
wmtsa-matlab-0.2.6/wmtsa/Tests/dwt
wmtsa-matlab-0.2.6/wmtsa/Tests/plotutils
wmtsa-matlab-0.2.6/wmtsa/Tests/utils
wmtsa-matlab-0.2.6/wmtsa/data
wmtsa-matlab-0.2.6/wmtsa/dwt
wmtsa-matlab-0.2.6/wmtsa/odwt/@omodwt
wmtsa-matlab-0.2.6/wmtsa/plotutils
wmtsa-matlab-0.2.6/wmtsa/signal
wmtsa-matlab-0.2.6/wmtsa/stats
wmtsa-matlab-0.2.6/wmtsa/third-party
wmtsa-matlab-0.2.6/wmtsa/utils
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.5.0.0 | 2 August 2015 Cove Sturtevant, Benjamin L. Ruddell [RELEASE VERSION 1.5] |
|
|
| 1.1.0.0 | Version 1.4 contains bug fixes and added features compared with the last release from April 2013, version 1.0. |
||
| 1.0.0.0 |