Abel Inversion Algorithm
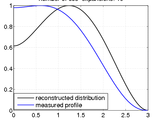
The reconstruction of the radial density distribution of a cylindrically symmetric object is a common task in different area of physics (e.g. plasma physics). Typically, optical measurements of objects like plasma columns or flames are integrated along the line of sight.
To obtain the underlying distribution from a measured projection, the inverse Abel transform has to be calculated.
This submission provides a Fourier-based algorithm which extracts the radial (2D) distribution from a one-dimensional projection measurement. The algorithm has been proposed and published by G. Pretzler (Z. Naturforsch. 46a, 639 (1991)). Compared to earlier approaches towards Abel inversion, this algorithm is relatively insensitive to noise and errors in the determination of the object's center (see G. Pretzler et al. , Z. Naturforsch. 47a, 955 (1994)).
The fundamental idea is to fit the whole measured profile to a set of cos-expansion-based integrals. (In the conventional approach, in contrast, the radial distribution is obtained by starting at the edges and incrementally iterating towards the center - making it more prone to errors.)
Cite As
Carsten Killer (2026). Abel Inversion Algorithm (https://www.mathworks.com/matlabcentral/fileexchange/43639-abel-inversion-algorithm), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > Signal Processing Toolbox > Transforms, Correlation, and Modeling > Transforms > Discrete Fourier and Cosine Transforms > Fast Fourier Transforms >
- Sciences > Physics > Plasma Physics >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.5.0.0 | Improvement of the integration scheme (thanks to Benjamin Tadsen). Using the coordinate transformation r=sqrt(t^2+x^2), the full integration limits can be evaluated (in previous versions, an epsilon was substracted to prevent diverging integrals). |
||
| 1.4.0.0 | I have been made aware of an error in the original article of G. Pretzler which results in missing factor 2. This factor 2 is now included in the code and I have deleted the paragraph in the description above which dealt with this issue. |
||
| 1.3.0.0 | Description has been updated. A paragraph regarding the interpretation of the result with respect to the real (physical) units in experimental situations has been added. |
||
| 1.1.0.0 | Instead of using lsqcurvefit (which requires the Optimization Toolbox), the final equation system can now be solved algebraically |
||
| 1.0.0.0 |