Estimating Market-Implied Value with Jump-Diffusion Models
By Somnath Chatterjee, Bank of England, and Ken Deeley, MathWorks
Estimating a firm’s true market value presents a challenge for financial professionals and technical analysts. Researchers at Bank of England have investigated this problem to understand how a firm’s true value is affected by periods of high market volatility.
A firm’s assets are subject to uncertainties such as profit flows and risk exposure. Similarly, default risk is driven by uncertain future asset values relative to promised payments on debt. Market value is typically estimated using mathematical models such as Black-Scholes/Merton, which are based on freely available but limited information about the firm, such as its market capitalization, the published face value of its debt, and the risk-free interest rate.
Financial crises have revealed shortcomings in these methodologies. One shortcoming is the inability of such models to include relatively infrequent but extreme movements, or jumps, in observed time series. While jumps are usually observed only occasionally, they occur frequently during financial crises or other periods of market uncertainty. For example, the plot in Figure 1 showing the market capitalization of a major UK bank in the first half of 2007 reveals several jumps of varying magnitudes (both upwards and downwards).

Figure 1. Market capitalization of a major UK bank in H1, 2007.
One way to assess the effect of jumps on market value is to use a jump-diffusion model. This is a combination of two stochastic processes, one to model the usual behavior of a series and another to model the presence of randomly occurring jumps. This article describes a workflow in which MATLAB®, Statistics and Machine Learning Toolbox™, and Signal Processing Toolbox™ are used to estimate the parameters of a jump-diffusion model for a firm’s hidden market value, starting with freely available market data. The resulting model can be used to derive other series of interest, such as the default probability and the credit spread.
Creating a Jump-Diffusion Model
Jump-diffusion models are based on the standard geometric Brownian motion (GBM) diffusion model. A GBM model has two parameters: the drift (average trend) and the diffusion (volatility) of the process. These parameters can be used to model the distribution of continuously compounded (log) returns \(R_{t}\) for a given price series \(P_{t}\):
\[R_t = {\text{log}} \frac{P_{t+∆t}}{P_t} \sim N \Biggl(\left(μ - \frac{σ^2}{2} \right)∆t, σ^2∆t \Biggr), \]
where \(∆t\) is the time increment, \(μ\) is the drift parameter, and \(σ\) is the diffusion parameter. The model assumes that the log returns are normally distributed with mean \((μ - {σ^2\over 2}) ∆t\) and variance \(σ^2∆t\).
Our jump-diffusion model extends the GBM model by introducing random jumps. The jumps \(J_{k}\) are a sequence of i.i.d. lognormal random variables: \(\text{log} J_{k} \sim N(μ_J,σ_J^2) \). The arrival of the jumps is modeled by a Poisson process \(N_{t}\) with rate \(λ\). The resulting dynamics of the time-series model are:
\[R_t = {\text{log}} \frac{P_t}{P_0} = \left(μ - \frac{σ^2}{2} \right)t + σW_t + \sum_{k=0}^{N_t}\ \text{log}J_k, \]
where \(W_{t}\) is a Wiener process. To estimate the model numerically, we discretize this continuous-time equation over time intervals \([t,t + ∆t]\). We assume that the time increment \(∆t\) is such that the probability of more than one jump occurring in \([t,t + ∆t]\) is negligible.
As with all mathematically complex models, jump-diffusion models present several computational challenges—for example, achieving convergence—and require careful analysis of the optimization process. With MATLAB, we can express the equations intuitively, with minimal coding; estimate the model parameters robustly; and track the convergence of the optimization procedures.
Estimating the Model Parameters
There are five model parameters to estimate:
- \(μ\) – the drift parameter of the GBM component
- \(σ\) – the diffusion parameter of the GBM component
- \(λ\) – the arrival rate of the jumps in the Poisson process
- \(μ_j\) – the lognormal location parameter for the jump sizes
- \(σ_j\) – the lognormal scale parameter for the jump sizes
We can estimate the last three parameters directly from the available time series data (assuming that the underlying market value of the company exhibits characteristics similar to those of the observable market capitalization). We can use the findchangepts function in Signal Processing Toolbox to automatically identify the points within a series where abrupt changes occur (Figure 2). In financial time series, we would expect structural changes to occur when the mean or standard deviation of the series changes significantly. Looking for points where the standard deviation changes is especially important when studying financial crises periods or other periods of high volatility.

Figure 2. Change points indicated by abrupt changes in the mean.
Estimation is based on the Black-Scholes/Merton model, where \(μ\) is a function of \(σ\). To do the optimization, we use the mle function in Statistics and Machine Learning Toolbox to perform maximum-likelihood estimation, specifying the negative log-likelihood function and the parameter bound constraints as inputs. The value of the likelihood function is ultimately determined by a single unknown parameter, \(σ\). Since market value is not observable, we begin the estimation process by fitting the jump-diffusion model to the observed market capitalization series and producing an initial estimate for the market value series. Using this initial estimate, we apply the process iteratively until the parameter values stabilize.
In models of implied market value and debt, the value of a firm is divided into assets that go to the equity holders and assets that go to the debt holders. When the debt falls due, if the assets are sufficient to repay the liabilities, then the excess value goes to the equity holders. If not, the equity holders receive nothing.
The value of debt is equivalent to a risk-free debt holding plus a short put option on the value of the assets: If the assets are more than enough to pay off the liabilities, then the debt holders receive the full value of the debt. If the assets are not enough to repay the liabilities, then the debt holders receive the full value of the assets. To the extent that the debt may not be repaid in full, it is deemed risky. Debt holders receive a put option premium in the form of a credit spread above the risk-free rate of interest in return for holding risky debt.
The asset value satisfies an implicit equation involving the market capitalization and the value of risky debt, which, in turn, is a function of the asset value and other variables, such as the risk-free interest rate. Within the maximum-likelihood estimation process, we solve this implicit equation for the asset value using the fzero function in MATLAB. After convergence, we plot the negative log-likelihood function in a neighborhood of the candidate solution point to verify that a local minimum point was identified by mle (Figure 3).
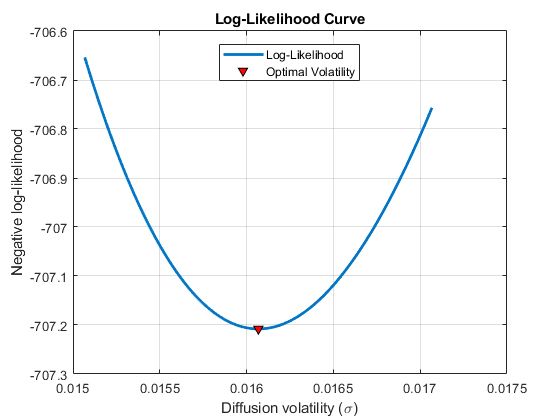
Figure 3. Log-likelihood curve in a small neighborhood around the solution point.
Inferring Market Value
After fitting the model, we can use it to infer the underlying market value of the asset and related quantities such as the value of the implicit put option on the asset and the asset’s leverage. Figure 4 shows these time series. As expected, we see that the value of a put option rapidly increases as the market capitalization and inferred market value of the asset drop. The leverage, a measure of the value-to-debt ratio, also increases as the asset value drops.

Figure 4. Inferred asset quantities from the jump-diffusion model.
Having developed and implemented a procedure for estimating the parameters of a jump-diffusion model, we can use the MATLAB Live Editor to share the results with colleagues as a live script. The process can be applied to various time series representing different assets and asset classes. The range of potential applications is broad, because many distinct financial series exhibit jumps during crisis periods and periods of high market uncertainty.
Published 2019