Modeling Machine Constraints in SimMechanics and Simulink
By Krishna Tamminana, MathWorks, Dallas C. Kennedy, MathWorks, and Arnav Mukherjee, MathWorks
All but the simplest rigid-body machines are designed to operate within kinematic constraints that restrict the motion of machine components independently of the forces imposed upon them. These constraints can be time-varying (rheonomic) or time-invariant (scleronomic). Dynamic analysis of these systems requires implementing such constraints between pairs of bodies. The equations representing them are typically higher-index differential algebraic equations that are very challenging to solve.
SimMechanics and Simulink let you model rigid-body machines using a graphical language rather than differential equations. Using blocks, you specify geometric and kinematic relations between bodies with localized body coordinate systems (CSs) and with joints, constraints, and drivers that add or remove degrees of freedom (DoFs) between the bodies. You can also apply forces or torques and initial conditions on the bodies through the joints. SimMechanics then simulates the machine’s motion by integrating its dynamics, eliminating the need to explicitly state or solve equations of motion.
This article presents four simple constrained motion mechanisms modeled with Constraint and Driver blocks:
It describes the principles behind each mechanism, focusing on the blocks that model each constrained kinematic pair. The related models are included in SimMechanics.
Constraint and Driver Blocks
SimMechanics includes a Constraints and Driver block library that lets you incorporate both scleronomic and rheonomic constraints in a mechanical model.
Constraint and unactuated driver blocks keep the constrained DoFs between the connected pair of bodies at their initial state, and thus impose scleronomic constraints. Actuated drivers implement rheonomic constraints by externally imposing a relative motion between pairs of bodies, starting at each body’s initial state. Constrained or driven pairs of bodies are still free to respond to externally applied forces or torques, but only in a way that is consistent with the imposed constraints.
The Rolling Sphere
The mech_rolling_sphere model represents the rolling motion of a sphere on a flat plane (immobile ground). The sphere and the ground constitute a constrained lower-order (point-contact) kinematic pair, a constraint commonly used in the simulation of wheels, tires, and bearing joints.
The sphere body is connected to the ground by a Custom Joint block at the point of contact (A). This joint allows the center of sphere to translate along the two prismatic axes (x- and y-axes), as well as roll and spin about A as a pivot, as defined in its dialog. The center of sphere (C) is free to translate in the xy plane. For the sphere to undergo pure rolling, the instantaneous linear velocity at A between the sphere and ground must be zero.
\(\vec{\omega}\) represents the angular velocity of the sphere, then the linear velocity of the point A is given by
\[\begin{equation}\begin{aligned}\vec{v}_A &= \vec{v}_C + \vec{\omega} \times (\vec{r}_A - \vec{r}_C)\\ \vec{\omega} &= \omega_X \vec{i} + \omega_Y \vec{j}\end{aligned}\end{equation}\tag{1}\]
(no spin about the z-axis). The constraint requires
\[\begin{aligned}\vec{r}_)A - \vec{r}_C &= -r \vec{k}\\ \vec{v}_A &= \vec{0}\end{aligned}\]
Hence
\[\begin{gather}\vec{v}_c = \omega_Y r \vec{i} - \omega_X r \vec{j} \tag{2a} \\ v_X = \omega_Y r \quad \text{and} \quad v_Y = -\omega_X r \tag{2b} \end{gather}\]
These relationships are implemented in the model with Velocity Driver blocks inside the Rolling Constraint subsystem. The First and Second rolling constraint block dialogs define the coefficients for the linear and angular velocities given by constraint set in (2b). The sphere rolls freely on the xy plane in response to the applied input force. The angular velocity components shown in the Angular Velocity scope block are similar to velocity components, as given by (2b).
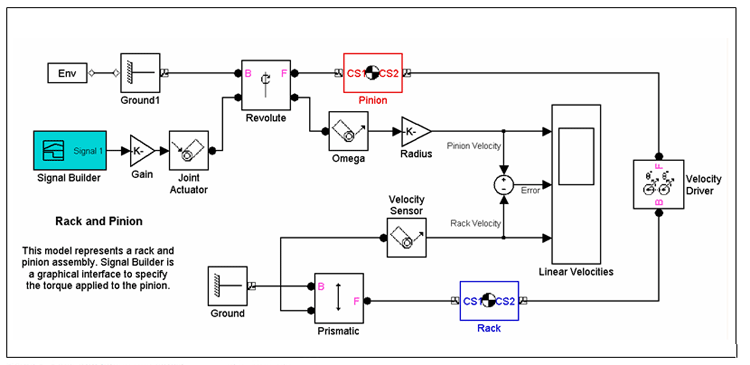
The Rack and Pinion
The mech_rack_pinion model represents a rack and pinion assembly that converts the rotational motion of the pinion to the translational motion of the rack. The pinion and the rack constitute the constrained kinematic pair. The line contact between the bodies makes for a higher-order (nonpoint) kinematic pair. A common application of the rack and pinion principle is the crank-slider steering mechanism in an automobile.
In the model, the pinion body is attached to the ground by a revolute joint at its center, as defined by the local body CS origin CS1. As a result, the pinion has a single rotational DoF about the z-axis as defined in the revolute joint. Input torque is applied to the pinion through the Joint Actuator block connected to the revolute joint. In this case, the torque is a simple step input that changes its magnitude from +1 to -1 at t = 3 seconds and holds until t = 10 seconds. The rack is connected to the ground through a prismatic joint that allows it to translate relative to the ground only along the x-axis.
The model has two DoFs, a rotational DoF for the pinion along z-axis and a translational DoF for the rack along the x-axis. The equations of motion are
\[\begin{align}T - r_p F &= I_p \ddot{\theta}\tag{3a}\\ F &= m\ddot{x}\tag{3b}\end{align}\]
where: \(T\) is the input torque applied on the pinion
\(F\) is the reaction force at the contact point between rack and pinion
\(I_p\) is the rotational inertia of the pinion along the z-axis
\(r_p\) is the pitch radius of the pinion
\(m\) is the mass of the rack
\(\theta\) is the rotation angle of the pinion body (radians)
\(x\) is the translational displacement of the rack
The local body CS origins CS2 on each body, representing the contact point between the pinion and rack, must have the same velocity. This constraint is modeled by the Velocity Driver block, whose dialog defines the velocity coefficients for the pinion and rack. Because the driver is unactuated, it holds the relationship between the constrained DoFs for the connected pair of bodies at their initial state. The rack-pinion constraint can be represented as
\[\dot{x} = r_p \dot{\theta}\tag{4}\]
Thus the coefficients for the Velocity Driver block are 1 and \(\frac{\pi r_p}{180}\). The latter form being necessary to convert the constraint angle from degrees to radians. (Radians are the natural mathematical units for angles.) By combining equation (3a,3b) with the rack-pinion constraint (4), you obtain
\[T = (I_p + m r_p^2)\ddot{\theta}\]
indicating that the rack and pinion system has only one independent degree of freedom.
In the simulation, the pinion rotates about its center while driving the rack along the x-axis. Also, the Linear Velocities scope block verifies the effect of the Velocity Driver: the relative velocity between the two bodies at the point of contact is always zero, as shown by the error signal.
Steering Mechanism
A more complex but familiar application using this principle is an automotive rack-and-pinion steering mechanism.
A rack-and-pinion gear set is enclosed in a metal tube, with each end of the rack protruding from the tube. A tie rod connects to each end of the rack. The pinion gear is attached to the steering shaft. When the steering wheel is turned the gear spins, moving the rack. The tie rod at each end of the rack connects to the steering arm on the spindle of the steering wheel.
The rack-and-pinion gear set converts the rotational motion of the steering wheel into the linear motion needed to turn the wheels. It provides a gear reduction, making it easier to turn the wheels.
Gears with Backlash
The mech_gears_backlash model illustrates how to simulate external gear pairs that transfer rotary motion from one shaft to another and how to include the effect of gear backlash. The mating gears constitute the constrained kinematic pair. The constraint is that a constant angular velocity ratio must be maintained between the gears. The line contact between the gears again makes for a higher-order (nonpoint) kinematic pair. Gears with backlash are common in automatic and manual transmissions and differentials.
The model illustrates two important points: First, to implement a gear pair in SimMechanics, you must mount the two constrained bodies on a fixed supporting body. Second, to incorporate the backlash effect, you must include an additional shaft body connected to one of the gear bodies through a revolute joint.
The base body is a fixed support connected to the ground. Two gear bodies, A and B, are connected to the ends of the base with the help of two revolute joints, introducing two DoFs. The Gear Constraint block enforces a constant angular velocity ratio between the two gears, A and B. The ratio is defined by the pitch circle radii for the two gears: \(r_A/r_B = \omega_B / \omega_A\), where \(r\) and \(\omega\) are the radii of the pitch circles and angular velocities of the respective gears indicated by the subscripts. The gear pair has a single independent DoF because of this gear constraint. The Joint Actuator block connected to the revolute joint actuates gear A with a predefined motion. In this case, the Motion Actuation subsystem specifies the instantaneous angle, angular velocity, and angular acceleration for gear A.
Backlash is introduced with the help of a shaft body connected to gear B through a revolute joint that represents an additional DoF. Motion is transmitted between the shaft and gear B by the Backlash Actuation subsystem only when the instantaneous angular motion of gear B exceeds the backlash angle limits. The Backlash Actuation subsystem consists of a Joint Actuator that transmits a nonzero force to the shaft body. The exact magnitude of the force transmitted depends on the difference between the angle of gear B and the backlash angle limit. The Force Law subsystem defines this force. For greater realism you can substitute your own force law model.
Gear A drives gear B at a constant angular velocity ratio. Here \(r_A/r_B = 3\), so gear B rotates three times faster than gear A. Gear B transmits motion to the shaft depending upon the difference between its angular position and backlash angle. The backlash effect is particularly striking at the instants when gear B reverses its direction of rotation and the shaft body lags behind gear B in reversing its direction.
The Cam-Belt Mechanism
The mech_cambelt model represents a cam-belt mechanism that coordinates the motion of a cam, a pulley, and the follower belt. The belt translates radially along a line passing through the axis of rotation of the cam. The model has two constrained kinematic pairs: The belt must move in a prescribed motion relative to the rotation of the cam, and the contact points between the belt and the pulley must have same velocity. This model is based on an example from robotic manufacturing, but the cam principle is commonly used in many machines.
The rotating cam body is connected to the ground through a revolute joint at the body CS origin CS1 coinciding with the cam’s center of gravity (CG). Thus the cam has a single rotational DoF about z-axis at its CG. The belt coupling body is free to move along the x-axis specified by the prismatic joint. As the translation axis of the belt passes through the axis of rotation of the cam, the belt is a radially translating follower.
The first constraint requires the belt’s body CS origin CS2 to move along a curve defined at the cam body CS2, and can be represented as \(x = f(r,\theta)\), where \(x\) is the displacement of the belt and \(f(r,\theta)\) is the surface profile of the cam. The belt body is connected to the cam body through a Point-Curve Constraint, which represents the constraint curve as a spline with breakpoints and appropriate endpoint conditions specified through the block dialog.
The second constraint is:
\[\dot{x} = r \dot{\theta}_p\]
where \(r\) is the radius of the pulley and \(\theta_p\) is the angular displacement of the pulley in radians. The pulley is connected to the ground at its center of gravity though a revolute joint. The Velocity Driver (Ideal Belt Constraint) that connects the pulley and belt bodies enforces the constant velocity constraint at the contact points. Since \(r = 1\) m this case, the coefficients of the Velocity Driver block dialog are 1 and 1.
The belt translates to and fro along the x-axis depending upon the cam profile as the cam rotates continuously in the clockwise (CW) direction. The pulley follows the belt motion when the belt reverses its direction of translation, the pulley reversing its sense of rotation from CW to counter-CW and vice versa.
The model’s belt can neither slip at the cam nor elastically deform. You can model both effects by adding Body and Joint blocks actuated with friction and elastic forces.
Conclusion
The models discussed in this article illustrate the five essential properties of Constraint and Driver blocks in SimMechanics:
-
Like Joint blocks, they must be connected between two bodies at one CS on each body.
-
Unlike Joint blocks, which add DoFs, they remove independent DoFs from a machine.
-
They constrain the DoFs between the connected pair of bodies by allowing or requiring them to move only in a prescribed motion. Specifically:
- Constraint blocks implement scleronomic constraints.
- Driver blocks implement both scleronomic and rheonomic constraints.
-
The directionality of Constraints and Drivers follows the same logic as Joint blocks.
-
Constraint and Driver blocks must occur in closed loops. A closed loop can include multiple Ground blocks.
To learn more about modeling in SimMechanics, see the User’s Guide.
Published 2006
References
-
Ghosh, A., and A. K. Mallik, Theory of Mechanisms and Machines, revised 3rd edition, Affiliated East-West Press (P) Ltd., New Delhi, 1998.