Acoustic Scene Recognition Using Late Fusion
This example shows how to create a multi-model late fusion system for acoustic scene recognition. The example trains a convolutional neural network (CNN) using mel spectrograms and an ensemble classifier using wavelet scattering. The example uses the TUT dataset for training and evaluation [1].
Introduction
Acoustic scene classification (ASC) is the task of classifying environments from the sounds they produce. ASC is a generic classification problem that is foundational for context awareness in devices, robots, and many other applications [1]. Early attempts at ASC used mel-frequency cepstral coefficients (mfcc) and Gaussian mixture models (GMMs) to describe their statistical distribution. Other popular features used for ASC include zero crossing rate, spectral centroid (spectralCentroid), spectral rolloff (spectralRolloffPoint), spectral flux (spectralFlux ), and linear prediction coefficients (lpc) [5]. Hidden Markov models (HMMs) were trained to describe the temporal evolution of the GMMs. More recently, the best performing systems have used deep learning, usually CNNs, and a fusion of multiple models. The most popular feature for top-ranked systems in the DCASE 2017 contest was the mel spectrogram (melSpectrogram). The top-ranked systems in the challenge used late fusion and data augmentation to help their systems generalize.
To illustrate a simple approach that produces reasonable results, this example trains a CNN using mel spectrograms and an ensemble classifier using wavelet scattering. The CNN and ensemble classifier produce roughly equivalent overall accuracy, but perform better at distinguishing different acoustic scenes. To increase overall accuracy, you merge the CNN and ensemble classifier results using late fusion.
Load Acoustic Scene Recognition Data Set
To run the example, you must first download the data set [1]. The full data set is approximately 15.5 GB. Depending on your machine and internet connection, downloading the data can take about 4 hours.
downloadFolder = tempdir; dataset = fullfile(downloadFolder,"TUT-acoustic-scenes-2017"); if ~datasetExists(dataset) disp("Downloading TUT-acoustic-scenes-2017 (15.5 GB) ...") HelperDownload_TUT_acoustic_scenes_2017(dataset); end
Read in the development set metadata as a table. Name the table variables FileName, AcousticScene, and SpecificLocation.
trainMetaData = readtable(fullfile(dataset,"TUT-acoustic-scenes-2017-development","meta"), ... Delimiter={'\t'}, ... ReadVariableNames=false); trainMetaData.Properties.VariableNames = ["FileName","AcousticScene","SpecificLocation"]; head(trainMetaData)
FileName AcousticScene SpecificLocation
__________________________ _____________ ________________
{'audio/b020_90_100.wav' } {'beach'} {'b020'}
{'audio/b020_110_120.wav'} {'beach'} {'b020'}
{'audio/b020_100_110.wav'} {'beach'} {'b020'}
{'audio/b020_40_50.wav' } {'beach'} {'b020'}
{'audio/b020_50_60.wav' } {'beach'} {'b020'}
{'audio/b020_30_40.wav' } {'beach'} {'b020'}
{'audio/b020_160_170.wav'} {'beach'} {'b020'}
{'audio/b020_170_180.wav'} {'beach'} {'b020'}
testMetaData = readtable(fullfile(dataset,"TUT-acoustic-scenes-2017-evaluation","meta"), ... Delimiter={'\t'}, ... ReadVariableNames=false); testMetaData.Properties.VariableNames = ["FileName","AcousticScene","SpecificLocation"]; head(testMetaData)
FileName AcousticScene SpecificLocation
__________________ _____________ ________________
{'audio/1245.wav'} {'beach'} {'b174'}
{'audio/1456.wav'} {'beach'} {'b174'}
{'audio/1318.wav'} {'beach'} {'b174'}
{'audio/967.wav' } {'beach'} {'b174'}
{'audio/203.wav' } {'beach'} {'b174'}
{'audio/777.wav' } {'beach'} {'b174'}
{'audio/231.wav' } {'beach'} {'b174'}
{'audio/768.wav' } {'beach'} {'b174'}
Note that the specific recording locations in the test set do not intersect with the specific recording locations in the development set. This makes it easier to validate that the trained models can generalize to real-world scenarios.
sharedRecordingLocations = intersect(testMetaData.SpecificLocation,trainMetaData.SpecificLocation);
disp("Number of specific recording locations in both train and test sets = " + numel(sharedRecordingLocations))Number of specific recording locations in both train and test sets = 0
The first variable of the metadata tables contains the file names. Concatenate the file names with the file paths.
trainFilePaths = fullfile(dataset,"TUT-acoustic-scenes-2017-development",trainMetaData.FileName); testFilePaths = fullfile(dataset,"TUT-acoustic-scenes-2017-evaluation",testMetaData.FileName);
There may be files listed in the metadata that are not present in the data set. Remove the file paths and acoustic scene labels that correspond to the missing files.
ads = audioDatastore(dataset,IncludeSubfolders=true); allFiles = ads.Files; trainIdxToRemove = ~ismember(trainFilePaths,allFiles); trainFilePaths(trainIdxToRemove) = []; trainLabels = categorical(trainMetaData.AcousticScene); trainLabels(trainIdxToRemove) = []; testIdxToRemove = ~ismember(testFilePaths,allFiles); testFilePaths(testIdxToRemove) = []; testLabels = categorical(testMetaData.AcousticScene); testLabels(testIdxToRemove) = [];
Create audio datastores for the train and test sets. Set the Labels property of the audioDatastore to the acoustic scene. Call countEachLabel to verify an even distribution of labels in both the train and test sets.
adsTrain = audioDatastore(trainFilePaths, ... Labels=trainLabels, ... IncludeSubfolders=true); display(countEachLabel(adsTrain))
15×2 table
Label Count
________________ _____
beach 312
bus 312
cafe/restaurant 312
car 312
city_center 312
forest_path 312
grocery_store 312
home 312
library 312
metro_station 312
office 312
park 312
residential_area 312
train 312
tram 312
adsTest = audioDatastore(testFilePaths, ... Labels=testLabels, ... IncludeSubfolders=true); display(countEachLabel(adsTest))
15×2 table
Label Count
________________ _____
beach 108
bus 108
cafe/restaurant 108
car 108
city_center 108
forest_path 108
grocery_store 108
home 108
library 108
metro_station 108
office 108
park 108
residential_area 108
train 108
tram 108
You can reduce the data set used in this example to speed up the run time at the cost of performance. In general, reducing the data set is a good practice for development and debugging. Set speedupExample to true to reduce the data set.
speedupExample =false; if speedupExample adsTrain = splitEachLabel(adsTrain,20); adsTest = splitEachLabel(adsTest,10); end trainLabels = adsTrain.Labels; testLabels = adsTest.Labels;
Call read to get the data and sample rate of a file from the train set. Audio in the database has consistent sample rate and duration. Normalize the audio and listen to it. Display the corresponding label.
[data,adsInfo] = read(adsTrain); data = data./max(data,[],"all"); fs = adsInfo.SampleRate; sound(data,fs) disp("Acoustic scene = " + string(adsTrain.Labels(1)))
Acoustic scene = beach
Call reset to return the datastore to its initial condition.
reset(adsTrain)
Feature Extraction for CNN
Each audio clip in the dataset consists of 10 seconds of stereo (left-right) audio. The feature extraction pipeline and the CNN architecture in this example are based on [3]. Hyperparameters for the feature extraction, the CNN architecture, and the training options were modified from the original paper using a systematic hyperparameter optimization workflow.
First, convert the audio to mid-side encoding. [3] suggests that mid-side encoded data provides better spatial information that the CNN can use to identify moving sources (such as a train moving across an acoustic scene).
dataMidSide = [sum(data,2),data(:,1)-data(:,2)];
Divide the signal into one-second segments with overlap. The final system uses a probability-weighted average on the one-second segments to predict the scene for each 10-second audio clip in the test set. Dividing the audio clips into one-second segments makes the network easier to train and helps prevent overfitting to specific acoustic events in the training set. The overlap helps to ensure all combinations of features relative to one another are captured by the training data. It also provides the system with additional data that can be mixed uniquely during augmentation.
segmentLength = 1; segmentOverlap = 0.5; [dataBufferedMid,~] = buffer(dataMidSide(:,1),round(segmentLength*fs),round(segmentOverlap*fs),"nodelay"); [dataBufferedSide,~] = buffer(dataMidSide(:,2),round(segmentLength*fs),round(segmentOverlap*fs),"nodelay"); dataBuffered = zeros(size(dataBufferedMid,1),size(dataBufferedMid,2)+size(dataBufferedSide,2)); dataBuffered(:,1:2:end) = dataBufferedMid; dataBuffered(:,2:2:end) = dataBufferedSide;
Use melSpectrogram to transform the data into a compact frequency-domain representation. Define parameters for the mel spectrogram as suggested by [3].
windowLength = 2048; samplesPerHop = 1024; samplesOverlap = windowLength - samplesPerHop; fftLength = 2*windowLength; numBands = 128;
melSpectrogram operates along channels independently. To optimize processing time, call melSpectrogram with the entire buffered signal.
spec = melSpectrogram(dataBuffered,fs, ... Window=hamming(windowLength,"periodic"), ... OverlapLength=samplesOverlap, ... FFTLength=fftLength, ... NumBands=numBands, ... ApplyLog=true);
Reshape the array to dimensions (Number of bands)-by-(Number of hops)-by-(Number of channels)-by-(Number of segments). When you feed an image into a neural network, the first two dimensions are the height and width of the image, the third dimension is the channels, and the fourth dimension separates the individual images.
X = reshape(spec,size(spec,1),size(spec,2),size(data,2),[]);
Call melSpectrogram without output arguments to plot the mel spectrogram of the mid channel for the first six of the one-second increments.
tiledlayout(3,2) for channel = 1:2:11 nexttile melSpectrogram(dataBuffered(:,channel),fs, ... Window=hamming(windowLength,"periodic"), ... OverlapLength=samplesOverlap, ... FFTLength=fftLength, ... NumBands=numBands, ... ApplyLog=true); title("Segment " + ceil(channel/2)) end
The helper function HelperSegmentedMelSpectrograms performs the feature extraction steps outlined above.
To apply the feature extraction steps to all files in the datastores, create transform datastores and specify the HelperSegmentedMelSpectrograms function as the transform. To speed up subsequent processing, use readall to read all of the files and place the extracted features in memory. Transform datastores can leverage parallel pools to speed up file reading and preprocessing if you have Parallel Computing Toolbox™.
tdsTrain = transform(adsTrain,@(x){HelperSegmentedMelSpectrograms(x,fs, ...
SegmentLength=segmentLength, ...
SegmentOverlap=segmentOverlap, ...
WindowLength=windowLength, ...
HopLength=samplesPerHop, ...
NumBands=numBands, ...
FFTLength=fftLength)});
xTrain = readall(tdsTrain,UseParallel=canUseParallelPool);Starting parallel pool (parpool) using the 'local' profile ... 16-Nov-2023 12:40:45: Job Queued. Waiting for parallel pool job with ID 1 to start ... 16-Nov-2023 12:41:46: Job Queued. Waiting for parallel pool job with ID 1 to start ... Connected to parallel pool with 6 workers.
xTrain = cat(4,xTrain{:});
tdsTest = transform(adsTest,@(x){HelperSegmentedMelSpectrograms(x,fs, ...
SegmentLength=segmentLength, ...
SegmentOverlap=segmentOverlap, ...
WindowLength=windowLength, ...
HopLength=samplesPerHop, ...
NumBands=numBands, ...
FFTLength=fftLength)});
xTest = readall(tdsTest,UseParallel=canUseParallelPool);
xTest = cat(4,xTest{:});Replicate the labels of the training and test sets so that they are in one-to-one correspondence with the segments.
numSegmentsPer10seconds = size(dataBuffered,2)/2; yTrain = repmat(trainLabels,1,numSegmentsPer10seconds)'; yTrain = yTrain(:); yTest = repmat(testLabels,1,numSegmentsPer10seconds)'; yTest = yTest(:);
Data Augmentation for CNN
The DCASE 2017 dataset contains a relatively small number of acoustic recordings for the task, and the development set and evaluation set were recorded at different specific locations. As a result, it is easy to overfit to the data during training. One popular method to reduce overfitting is mixup. In mixup, you augment your dataset by mixing the features of two different classes. When you mix the features, you mix the labels in equal proportion. That is:
Mixup was reformulated by [2] as labels drawn from a probability distribution instead of mixed labels. The implementation of mixup in this example is a simplified version of mixup: each spectrogram is mixed with a spectrogram of a different label with lambda set to 0.5. The original and mixed datasets are combined for training.
xTrainExtra = xTrain; yTrainExtra = yTrain; lambda = 0.5; for ii = 1:size(xTrain,4) % Find all available spectrograms with different labels. availableSpectrograms = find(yTrain~=yTrain(ii)); % Randomly choose one of the available spectrograms with a different label. numAvailableSpectrograms = numel(availableSpectrograms); idx = randi([1,numAvailableSpectrograms]); % Mix. xTrainExtra(:,:,:,ii) = lambda*xTrain(:,:,:,ii) + (1-lambda)*xTrain(:,:,:,availableSpectrograms(idx)); % Specify the label as randomly set by lambda. if rand > lambda yTrainExtra(ii) = yTrain(availableSpectrograms(idx)); end end xTrain = cat(4,xTrain,xTrainExtra); yTrain = [yTrain;yTrainExtra];
Call summary to display the distribution of labels for the augmented training set.
summary(yTrain)
beach 11769
bus 11904
cafe/restaurant 11873
car 11820
city_center 11886
forest_path 11936
grocery_store 11914
home 11923
library 11817
metro_station 11804
office 11922
park 11871
residential_area 11704
train 11773
tram 11924
Define and Train CNN
Define the CNN architecture. This architecture is based on [1] and modified through trial and error. See List of Deep Learning Layers (Deep Learning Toolbox) to learn more about deep learning layers available in MATLAB®.
imgSize = [size(xTrain,1),size(xTrain,2),size(xTrain,3)]; numF = 32; layers = [ ... imageInputLayer(imgSize) batchNormalizationLayer convolution2dLayer(3,numF,Padding="same") batchNormalizationLayer reluLayer convolution2dLayer(3,numF,Padding="same") batchNormalizationLayer reluLayer maxPooling2dLayer(3,Stride=2,Padding="same") convolution2dLayer(3,2*numF,Padding="same") batchNormalizationLayer reluLayer convolution2dLayer(3,2*numF,Padding="same") batchNormalizationLayer reluLayer maxPooling2dLayer(3,Stride=2,Padding="same") convolution2dLayer(3,4*numF,Padding="same") batchNormalizationLayer reluLayer convolution2dLayer(3,4*numF,Padding="same") batchNormalizationLayer reluLayer maxPooling2dLayer(3,Stride=2,Padding="same") convolution2dLayer(3,8*numF,Padding="same") batchNormalizationLayer reluLayer convolution2dLayer(3,8*numF,Padding="same") batchNormalizationLayer reluLayer globalAveragePooling2dLayer dropoutLayer(0.5) fullyConnectedLayer(15) softmaxLayer];
Define trainingOptions (Deep Learning Toolbox) for the CNN. These options are based on [3] and modified through a systematic hyperparameter optimization workflow.
miniBatchSize = 128; tuneme = 128; lr = 0.05*miniBatchSize/tuneme; options = trainingOptions( ... "sgdm", ... Momentum=0.9, ... L2Regularization=0.005, ... ... MiniBatchSize=miniBatchSize, ... MaxEpochs=8, ... Shuffle="every-epoch", ... ... Plots="training-progress", ... Verbose=false, ... Metrics="accuracy", ... ... InitialLearnRate=lr, ... LearnRateSchedule="piecewise", ... LearnRateDropPeriod=2, ... LearnRateDropFactor=0.2, ... ... ValidationData={xTest,yTest}, ... ValidationFrequency=floor(size(xTrain,4)/miniBatchSize));
Call trainnet to train the network.
trainedNet = trainnet(xTrain,yTrain,layers,"crossentropy",options);
Evaluate CNN
Call minibatchpredict to predict responses from the trained network using the held-out test set.
cnnResponsesPerSegment = minibatchpredict(trainedNet,xTest);
Average the responses over each 10-second audio clip.
classes = unique(trainLabels); numFiles = numel(testLabels); counter = 1; cnnResponses = zeros(numFiles,numel(classes)); for channel = 1:numFiles cnnResponses(channel,:) = sum(cnnResponsesPerSegment(counter:counter+numSegmentsPer10seconds-1,:),1)/numSegmentsPer10seconds; counter = counter + numSegmentsPer10seconds; end
For each 10-second audio clip, choose the maximum of the predictions, then map it to the corresponding predicted location.
[~,classIdx] = max(cnnResponses,[],2); cnnPredictedLabels = classes(classIdx);
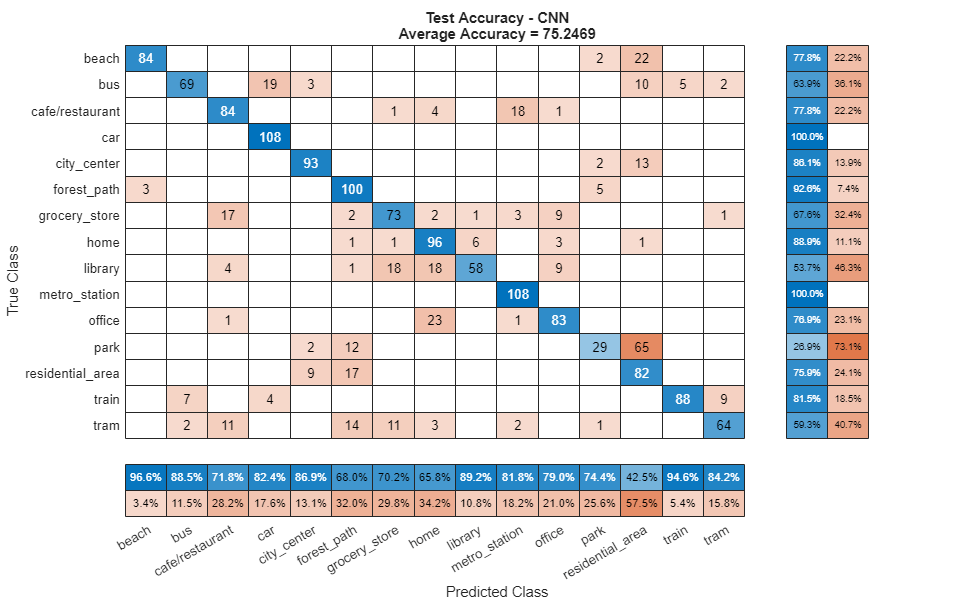
Call confusionchart (Deep Learning Toolbox) to visualize the accuracy on the test set.
figure(Units="normalized",Position=[0.2 0.2 0.5 0.5]) confusionchart(testLabels,cnnPredictedLabels, ... title=["Test Accuracy - CNN","Average Accuracy = " + mean(testLabels==cnnPredictedLabels)*100], ... ColumnSummary="column-normalized",RowSummary="row-normalized");
Feature Extraction for Ensemble Classifier
Wavelet scattering has been shown in [4] to provide a good representation of acoustic scenes. Define a waveletScattering (Wavelet Toolbox) object. The invariance scale and quality factors were determined through trial and error.
sf = waveletScattering(SignalLength=size(data,1), ... SamplingFrequency=fs, ... InvarianceScale=0.75, ... QualityFactors=[4 1]);
Convert the audio signal to mono, and then call featureMatrix (Wavelet Toolbox) to return the scattering coefficients for the scattering decomposition framework, sf.
dataMono = mean(data,2);
scatteringCoeffients = featureMatrix(sf,dataMono,Transform="log");Average the scattering coefficients over the 10-second audio clip.
featureVector = mean(scatteringCoeffients,2);
disp("Number of wavelet features per 10-second clip = " + numel(featureVector));Number of wavelet features per 10-second clip = 286
The helper function HelperWaveletFeatureVector performs the above steps. Use a transform datastore to parallelize the feature extraction. Extract wavelet feature vectors for the train and test sets.
scatteringTrain = transform(adsTrain,@(x)HelperWaveletFeatureVector(x,sf)); xTrain = readall(scatteringTrain,UseParallel=canUseParallelPool); xTrain = (reshape(xTrain,numel(featureVector),[]))';
scatteringTest = transform(adsTest,@(x)HelperWaveletFeatureVector(x,sf)); xTest = readall(scatteringTest,UseParallel=canUseParallelPool); xTest = (reshape(xTest,numel(featureVector),[]))';
Define and Train Ensemble Classifier
Use fitcensemble to create a trained classification ensemble model (ClassificationEnsemble).
subspaceDimension = min(150,size(xTrain,2) - 1); numLearningCycles = 30; classificationEnsemble = fitcensemble(xTrain,trainLabels, ... Method="Subspace", ... NumLearningCycles=numLearningCycles, ... Learners="discriminant", ... NPredToSample=subspaceDimension, ... ClassNames=removecats(unique(trainLabels)));
Evaluate Ensemble Classifier
For each 10-second audio clip, call predict to return the labels and the weights, then map it to the corresponding predicted location. Call confusionchart (Deep Learning Toolbox) to visualize the accuracy on the test set.
[waveletPredictedLabels,waveletResponses] = predict(classificationEnsemble,xTest); figure(Units="normalized",Position=[0.2 0.2 0.5 0.5]) confusionchart(testLabels,waveletPredictedLabels, ... title=["Test Accuracy - Wavelet Scattering","Average Accuracy = " + mean(testLabels==waveletPredictedLabels)*100], ... ColumnSummary="column-normalized",RowSummary="row-normalized");
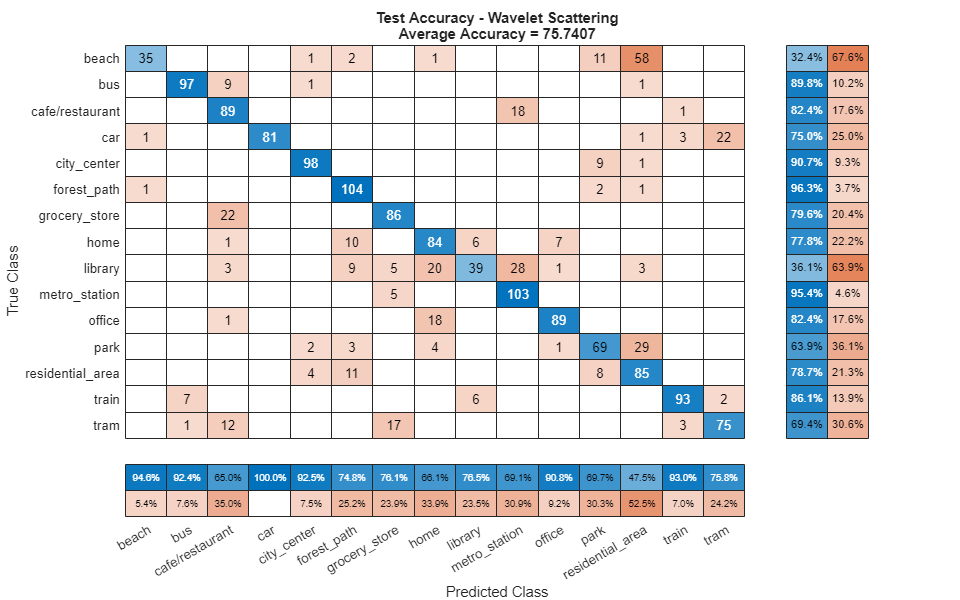
fprintf('Average accuracy of classifier = %0.2f\n',mean(testLabels==waveletPredictedLabels)*100)Average accuracy of classifier = 75.74
Apply Late Fusion
For each 10-second clip, calling predict on the wavelet classifier and the CNN returns a vector indicating the relative confidence in their decision. Multiply the waveletResponses with the cnnResponses to create a late fusion system.
fused = waveletResponses.*cnnResponses; [~,classIdx] = max(fused,[],2); predictedLabels = classes(classIdx);
Evaluate Late Fusion
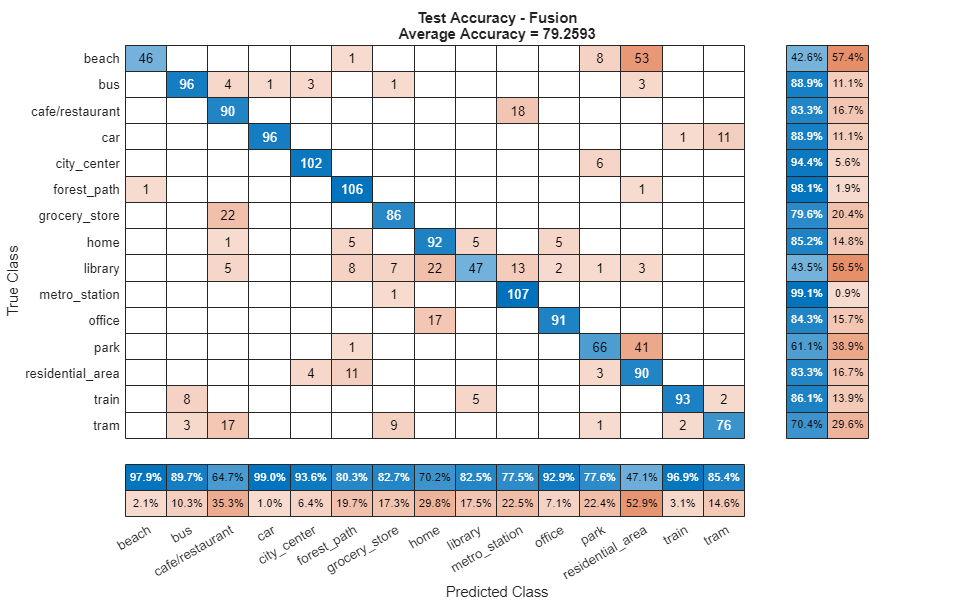
Call confusionchart to visualize the fused classification accuracy.
figure(Units="normalized",Position=[0.2 0.2 0.5 0.5]) confusionchart(testLabels,predictedLabels, ... Title=["Test Accuracy - Fusion","Average Accuracy = " + mean(testLabels==predictedLabels)*100], ... ColumnSummary="column-normalized",RowSummary="row-normalized");
Supporting Functions
HelperSegmentedMelSpectrograms
function X = HelperSegmentedMelSpectrograms(x,fs,options) % Copyright 2019-2023 The MathWorks, Inc. arguments x fs options.WindowLength = 1024 options.HopLength = 512 options.NumBands = 128 options.SegmentLength = 1 options.SegmentOverlap = 0 options.FFTLength = 1024 end x = [sum(x,2),x(:,1)-x(:,2)]; x = x./max(max(x)); [xb_m,~] = buffer(x(:,1),round(options.SegmentLength*fs),round(options.SegmentOverlap*fs),"nodelay"); [xb_s,~] = buffer(x(:,2),round(options.SegmentLength*fs),round(options.SegmentOverlap*fs),"nodelay"); xb = zeros(size(xb_m,1),size(xb_m,2)+size(xb_s,2)); xb(:,1:2:end) = xb_m; xb(:,2:2:end) = xb_s; spec = melSpectrogram(xb,fs, ... Window=hamming(options.WindowLength,"periodic"), ... OverlapLength=options.WindowLength - options.HopLength, ... FFTLength=options.FFTLength, ... NumBands=options.NumBands, ... FrequencyRange=[0,floor(fs/2)], ... ApplyLog=true); X = reshape(spec,size(spec,1),size(spec,2),size(x,2),[]); end
HelperWaveletFeatureExtractor
function features = HelperWaveletFeatureVector(x,sf) % Copyright 2019-2023 The MathWorks, Inc. if canUseGPU x = gpuArray(x); end x = mean(x,2); features = featureMatrix(sf,x,Transform="log"); features = gather(mean(features,2)); end
References
[1] A. Mesaros, T. Heittola, and T. Virtanen. Acoustic Scene Classification: an Overview of DCASE 2017 Challenge Entries. In proc. International Workshop on Acoustic Signal Enhancement, 2018.
[2] Huszar, Ferenc. "Mixup: Data-Dependent Data Augmentation." InFERENCe. November 03, 2017. Accessed January 15, 2019. https://www.inference.vc/mixup-data-dependent-data-augmentation/.
[3] Han, Yoonchang, Jeongsoo Park, and Kyogu Lee. "Convolutional neural networks with binaural representations and background subtraction for acoustic scene classification." the Detection and Classification of Acoustic Scenes and Events (DCASE) (2017): 1-5.
[4] Lostanlen, Vincent, and Joakim Anden. Binaural scene classification with wavelet scattering. Technical Report, DCASE2016 Challenge, 2016.
[5] A. J. Eronen, V. T. Peltonen, J. T. Tuomi, A. P. Klapuri, S. Fagerlund, T. Sorsa, G. Lorho, and J. Huopaniemi, "Audio-based context recognition," IEEE Trans. on Audio, Speech, and Language Processing, vol 14, no. 1, pp. 321-329, Jan 2006.
