SI Core Engine
Spark-ignition engine from intake to exhaust port
Libraries:
Powertrain Blockset /
Propulsion /
Combustion Engine Components /
Core Engine
Description
The SI Core Engine block implements a spark-ignition (SI) engine from intake to exhaust port. You can use the block in larger vehicle models, hardware-in-the-loop (HIL) engine control design, or vehicle-level fuel economy and performance simulations.
The SI Core Engine block calculates:
Brake torque
Fuel flow
Port gas mass flow, including exhaust gas recirculation (EGR)
Air-fuel ratio (AFR)
Exhaust temperature and exhaust mass flow rate
Engine-out (EO) exhaust emissions
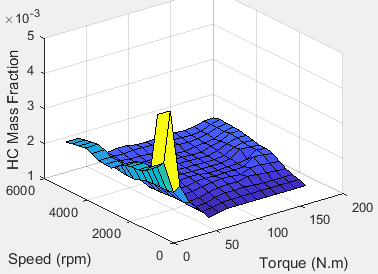
Hydrocarbon (HC)
Carbon monoxide (CO)
Nitric oxide and nitrogen dioxide (NOx)
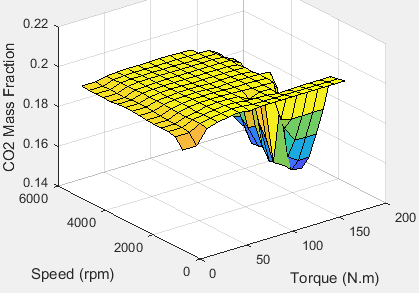
Carbon dioxide (CO2)
Particulate matter (PM)
Air Mass Flow
To calculate engine air mass flow, configure the SI engine to use either of these air mass flow models.
| Air Mass Flow Model | Description |
|---|---|
| SI Engine Speed-Density Air Mass Flow Model |
Uses the speed-density equation to calculate the engine air mass flow, relating the engine air mass flow to the intake manifold pressure and engine speed. Consider using this air mass flow model in engines with fixed valvetrain designs. |
| SI Engine Dual-Independent Cam Phaser Air Mass Flow Model |
To calculate the engine air mass flow, the dual-independent cam phaser model uses:
In contrast to typical embedded air mass flow calculations based on direct air mass flow measurement with an air mass flow (MAF) sensor, this air mass flow model offers:
|
Brake Torque
To calculate the brake torque, configure the SI engine to use either of these torque models.
| Brake Torque Model | Description |
|---|---|
| SI Engine Torque Structure Model | For the structured brake torque calculation, the SI engine uses tables for the inner torque, friction torque, optimal spark, spark efficiency, and lambda efficiency. If you select Crank angle pressure and torque on the block Torque tab, you can:
|
| SI Engine Simple Torque Model |
For the simple brake torque calculation, the SI engine block uses a torque lookup table map that is a function of engine speed and load. |
Fuel Flow
To calculate the fuel flow, the SI Core Engine block uses fuel injector characteristics and fuel injector pulse-width.
To calculate the fuel economy for high-fidelity models, the block uses the volumetric fuel flow.
The equation uses these variables.
| Fuel mass flow, g/s | |
| Engine rotational speed, rad/s | |
Crankshaft revolutions per power stroke, rev/stroke | |
Fuel injector slope, mg/ms | |
Fuel injector pulse-width, ms | |
Number of engine cylinders | |
| N | Engine speed, rpm |
| Sgfuel | Specific gravity of fuel |
| Qfuel | Volumetric fuel flow |
The block uses the internal signal FlwDir to track the direction of the flow.
Air-Fuel Ratio
To calculate the air-fuel (AFR) ratio, the CI Core Engine and SI Core Engine blocks implement this equation.
The CI Core Engine uses this equation to calculate the relative AFR.
To calculate the exhaust gas recirculation (EGR), the blocks implement this equation. The calculation expresses the EGR as a percent of the total intake port flow.
The equations use these variables.
Air-fuel ratio | |
| AFRs | Stoichiometric air-fuel ratio |
Engine air mass flow | |
Fuel mass flow | |
λ | Relative AFR |
| yintk,b | Intake burned mass fraction |
| EGRpct | EGR percent |
Recirculated burned gas mass flow rate |
Exhaust
The block calculates the:
Exhaust gas temperature
Exhaust gas-specific enthalpy
Exhaust gas mass flow rate
Engine-out (EO) exhaust emissions:
Hydrocarbon (HC)
Carbon monoxide (CO)
Nitric oxide and nitrogen dioxide (NOx)
Carbon dioxide (CO2)
Particulate matter (PM)
The exhaust temperature determines the specific enthalpy.
The exhaust mass flow rate is the sum of the intake port air mass flow and the fuel mass flow.
To calculate the exhaust emissions, the block multiplies the emission mass fraction by the exhaust mass flow rate. To determine the emission mass fractions, the block uses lookup tables that are functions of the engine torque and speed.
The fraction of air and fuel entering the intake port, injected fuel, and stoichiometric AFR determine the air mass fraction that exits the exhaust.
If the engine is operating at the stoichiometric or fuel rich AFR, no air exits the exhaust. Unburned hydrocarbons and burned gas comprise the remainder of the exhaust gas. This equation determines the exhaust burned gas mass fraction.
The equations use these variables.
Engine exhaust temperature | |
Exhaust manifold inlet-specific enthalpy | |
Exhaust gas specific heat | |
Intake port air mass flow rate | |
Fuel mass flow rate | |
Exhaust mass flow rate | |
Intake fuel mass fraction | |
| yexh,i | Exhaust mass fraction for i = CO2, CO, HC, NOx, air, burned gas, and PM |
Exhaust mass flow rate for i = CO2, CO, HC, NOx, air, burned gas, and PM | |
| Tbrake | Engine brake torque |
| N | Engine speed |
| yexh,air | Exhaust air mass fraction |
| yexh,b | Exhaust air burned mass fraction |
Power Accounting
For the power accounting, the block implements equations that depend on Torque model.
When you set Torque model to Simple Torque Lookup, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Intake heat flow | |
PwrExhHeatFlw | Exhaust heat flow | |||
PwrCrkshft | Crankshaft power | |||
| PwrFuel | Fuel input power | ||
PwrLoss | All losses | |||
| Not used | |||
When you set Torque model to Torque Structure, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Intake heat flow | |
PwrExhHeatFlw | Exhaust heat flow | |||
PwrCrkshft | Crankshaft power | |||
| PwrFuel | Fuel input power | ||
PwrFricLoss | Friction loss | |||
PwrPumpLoss | Pumping loss | |||
PwrHeatTrnsfrLoss | Heat transfer loss | |||
| Not used | |||
| hexh | Exhaust manifold inlet-specific enthalpy |
| hintk | Intake port specific enthalpy |
Intake port air mass flow rate | |
Fuel mass flow rate | |
Exhaust mass flow rate | |
| ω | Engine speed |
| Tbrake | Brake torque |
| Tpump | Engine pumping work offset to inner torque |
| Tfric | Engine friction torque |
| LHV | Fuel lower heating value |
Examples
Ports
Input
Output
Parameters
References
[1] Gerhardt, J., Hönninger, H., and Bischof, H., A New Approach to Functional and Software Structure for Engine Management Systems — BOSCH ME7. SAE Technical Paper 980801, 1998.
[2] Heywood, John B. Internal Combustion Engine Fundamentals. New York: McGraw-Hill, 1988.
Extended Capabilities
Version History
Introduced in R2017a