Spatial Multiplexing
This example shows spatial multiplexing schemes wherein the data stream is subdivided into independent sub-streams, one for each transmit antenna employed. As a consequence, these schemes provide a multiplexing gain and do not require explicit orthogonalization as needed for space-time block coding.
Spatial multiplexing requires powerful decoding techniques at the receiver though. Of the many proposed [ 1 ], this example highlights two ordered Successive Interference Cancellation (SIC) detection schemes. These schemes are similar to the original Bell Labs Layered Space-Time (BLAST) techniques as per [ 2 ], [ 3 ].
For expositional benefits the example uses the basic 2x2 MIMO system employing two transmit and two receive antennas. For an uncoded QPSK modulated system it employs flat Rayleigh fading over independent transmit-receive links. At the receiver end, we assume perfect channel knowledge with no feedback to the transmitter, i.e., an open-loop spatial multiplexing system.
The example shows two nonlinear interference cancellation methods - Zero-Forcing (ZF) and Minimum-Mean-Square-Error (MMSE) - with symbol cancellation and compares their performance with the Maximum-Likelihood (ML) optimum receiver.
Simulation
Define common simulation parameters and then and set up the simulation.
N = 2; % Number of transmit antennas M = 2; % Number of receive antennas EbNoVec = 2:3:8; % Eb/No in dB bps = 2; % Bits per symbol M = 2^bps; % Constellation size
Create a local random stream to be used by random number generators for repeatability.
stream = RandStream('mt19937ar'); % Calculate SNR from EbNo for each independent transmission link snrIndB = convertSNR(EbNoVec,'ebno','BitsPerSymbol',bps); snrLinear = 10.^(0.1*snrIndB); % Create error rate calculation System objects for 3 different receivers zfBERCalc = comm.ErrorRate; mmseBERCalc = comm.ErrorRate; mlBERCalc = comm.ErrorRate; % Get all bit and symbol combinations for ML receiver allBits = int2bit(0:2^(bps*N)-1,bps*N); allTxSig = reshape(pskmod(allBits(:),M,0,InputType="bit"), ... N,2^(bps*N)); % Pre-allocate variables to store BER results for speed [BER_ZF,BER_MMSE,BER_ML] = deal(zeros(length(EbNoVec),3));
The simulation loop below simultaneously evaluates the BER performance of the three receiver schemes for each Eb/No value using the same data and channel realization. A short range of Eb/No values are used for simulation purposes. Results for a larger range, using the same code, are presented later.
% Set up a figure for visualizing BER results fig = figure; grid on; hold on; ax = fig.CurrentAxes; ax.YScale = 'log'; xlim([EbNoVec(1)-0.01 EbNoVec(end)]); ylim([1e-3 1]); xlabel('Eb/No (dB)'); ylabel('BER'); fig.NumberTitle = 'off'; fig.Name = 'Spatial Multiplexing'; title('2x2 Uncoded QPSK System'); set(fig,'DefaultLegendAutoUpdate','off'); % Loop over selected EbNo points for idx = 1:length(EbNoVec) % Reset error rate calculation System objects reset(zfBERCalc); reset(mmseBERCalc); reset(mlBERCalc); while (BER_ZF(idx, 3) < 1e5) && ((BER_MMSE(idx, 2) < 100) || ... (BER_ZF(idx, 2) < 100) || (BER_ML(idx, 2) < 100)) % Create random bit vector to modulate msg = randi(stream,[0 1],[N*bps,1]); % Modulate data txSig = pskmod(msg,M,0,InputType="bit"); % Flat Rayleigh fading channel with independent links rayleighChan = (randn(stream,M,N) + 1i*randn(stream,M,N))/sqrt(2); % Add noise to faded data rxSig = awgn(rayleighChan*txSig,snrIndB(idx),0,stream); % ZF-SIC receiver r = rxSig; H = rayleighChan; % Assume perfect channel estimation % Initialization estZF = zeros(N*bps,1); orderVec = 1:N; k = N+1; % Start ZF nulling loop for n = 1:N % Shrink H to remove the effect of the last decoded symbol H = H(:,[1:k-1,k+1:end]); % Shrink order vector correspondingly orderVec = orderVec(1,[1:k-1,k+1:end]); % Select the next symbol to be decoded G = (H'*H) \ eye(N-n+1); % Same as inv(H'*H), but faster [~, k] = min(diag(G)); symNum = orderVec(k); % Hard decode the selected symbol decBits = pskdemod(G(k,:) * H' * r,M,0,OutputType="bit"); estZF(bps * (symNum-1) + (1:bps)) = decBits; % Subtract the effect of the last decoded symbol from r if n < N r = r - H(:, k) * pskmod(decBits,M,0,InputType="bit"); end end % MMSE-SIC receiver r = rxSig; H = rayleighChan; % Initialization estMMSE = zeros(N*bps, 1); orderVec = 1:N; k = N+1; % Start MMSE nulling loop for n = 1:N H = H(:, [1:k-1,k+1:end]); orderVec = orderVec(1, [1:k-1,k+1:end]); % Order algorithm (matrix G calculation) is the only difference % with the ZF-SIC receiver G = (H'*H + ((N-n+1)/snrLinear(idx))*eye(N-n+1)) \ eye(N-n+1); [~, k] = min(diag(G)); symNum = orderVec(k); decBits = pskdemod(G(k,:) * H' * r,M,0,OutputType="bit"); estMMSE(bps * (symNum-1) + (1:bps)) = decBits; if n < N r = r - H(:, k) * pskmod(decBits,M,0,InputType="bit"); end end % ML receiver r = rxSig; H = rayleighChan; [~, k] = min(sum(abs(repmat(r,[1,2^(bps*N)]) - H*allTxSig).^2)); estML = allBits(:,k); % Update BER BER_ZF(idx,:) = zfBERCalc(msg,estZF); BER_MMSE(idx,:) = mmseBERCalc(msg,estMMSE); BER_ML(idx,:) = mlBERCalc(msg,estML); end % Plot results semilogy(EbNoVec(1:idx),BER_ZF(1:idx,1),'r*', ... EbNoVec(1:idx),BER_MMSE(1:idx,1),'bo', ... EbNoVec(1:idx),BER_ML(1:idx,1),'gs'); legend('ZF-SIC','MMSE-SIC','ML'); drawnow; end % Draw the lines semilogy(EbNoVec,BER_ZF(:,1),'r-', ... EbNoVec,BER_MMSE(:,1),'b-', ... EbNoVec,BER_ML(:,1),'g-'); hold off;
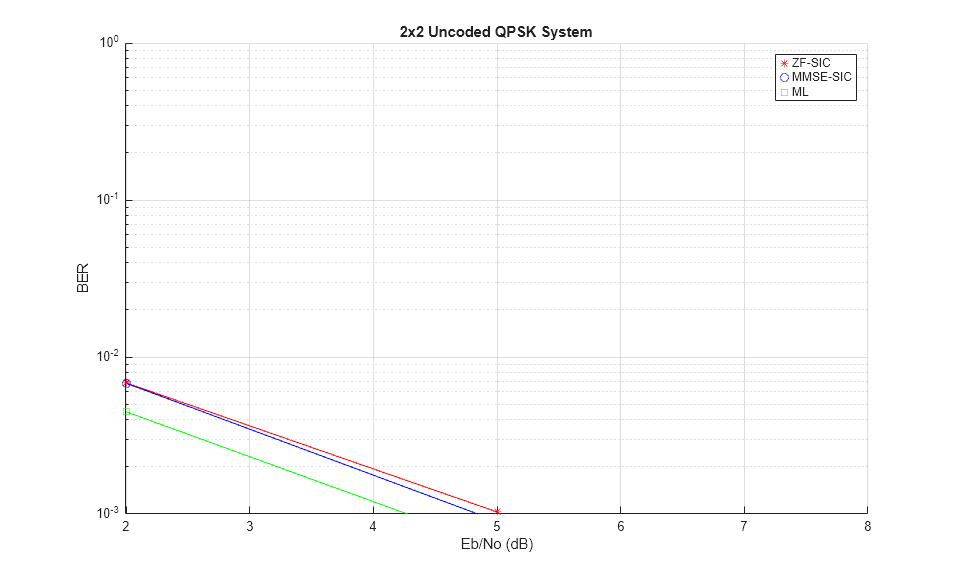
We observe that the ML receiver is the best in performance followed by the MMSE-SIC and ZF-SIC receivers, as also seen in [ 4 ]. In terms of receiver complexity, ML grows exponentially with the number of transmit antennas while the ZF-SIC and MMSE-SIC are linear receivers combined with successive interference cancellation. Optimized ZF-SIC and MMSE-SIC algorithms for reduced complexity can be found in [ 5 ].
Simulation results comparing the three schemes for a larger range of Eb/No values are displayed next. These curves allow you to gauge the diversity order attained from the slope of the BER curve.
openfig('spatMuxResults.fig');

Some areas of further exploration would be to try these methods for a larger number of antennas, with and without channel estimation.
Selected References
George Tsoulos, Ed., "MIMO System Technology for Wireless Communications", CRC Press, Boca Raton, FL, 2006.
G. J. Foschini, "Layered space-time architecture for wireless communication in a fading environment when using multiple antennas," The Bell Sys. Tech. Journal, 1996, No. 1, pp. 41-59.
P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela, "V-BLAST: An Architecture for realizing very high data rates over the rich scattering wireless channel," 1998 URSI International Symposium on Signals, Systems, and Electronics, 29 Sep.-2 Oct. 1998, pp. 295-300.
X. Li, H. C. Huang, A. Lozano, G. J. Foschini, "Reduced-complexity detection algorithms for systems using multi-element arrays", IEEE® Global Telecommunications Conference, 2000. Volume 2, 27 Nov.-1 Dec. 2000, pp. 1072-76.
Y. Shang and X.-G. Xia, "On fast recursive algorithms for V-BLAST with optimal ordered SIC detection," IEEE Trans. Wireless Communications, vol. 8, no. 6, pp. 2860-2865, Jun. 2009.