comm.DPD
Digital predistorter
Description
The comm.DPD
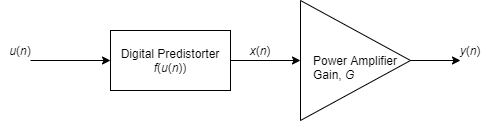
System object™ applies digital predistortion (DPD) to a complex baseband signal by using a
memory polynomial to compensate for nonlinearities in a power amplifier. For more information,
see Digital Predistortion and Optimizing Estimator Polynomial Degree and Memory Depth.
To predistort signals:
Create the
comm.DPDobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
dpd = comm.DPD
dpd = comm.DPD(Name,Value)comm.DPD('PolynomialType','Cross-term memory polynomial') configures
the predistorter System object to predistort the input signal by using a memory polynomial with cross
terms. Enclose each property name in quotes.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Morgan, Dennis R., Zhengxiang Ma, Jaehyeong Kim, Michael G. Zierdt, and John Pastalan. "A Generalized Memory Polynomial Model for Digital Predistortion of Power Amplifiers." IEEE® Transactions on Signal Processing. Vol. 54, Number 10, October 2006, pp. 3852–3860.
[2] M. Schetzen. The Volterra and Wiener Theories of Nonlinear Systems. New York: Wiley, 1980.
Extended Capabilities
Version History
Introduced in R2019a