MSK Signal Recovery
Model channel impairments such as timing phase offset, carrier frequency offset, and carrier phase offset for a minimum shift keying (MSK) signal. Use comm.MSKTimingSynchronizer and comm.CarrierSynchronizer System objects to synchronize such signals at the receiver. The MSK timing synchronizer recovers the timing offset, while a carrier synchronizer recovers the carrier frequency and phase offsets.
Initialize system variables by running the MATLAB® script configureMSKSignalRecoveryEx. Define the logical control variable recoverTimingPhase to enable timing phase recovery, and recoverCarrier to enable carrier frequency and phase recovery.
configureMSKSignalRecoveryEx; recoverTimingPhase = true; recoverCarrier = true;
Modeling Channel Impairments
Specify the sample delay, timingOffset, that the channel model applies. Create a variable fractional delay object to introduce the timing delay to the transmitted signal.
timingOffset = 0.2; varDelay = dsp.VariableFractionalDelay;
Create a comm.PhaseFrequencyOffset System object™ to introduce carrier phase and frequency offsets to a modulated signal. Because the MSK modulator upsamples the transmitted symbols, set the SampleRate property to the ratio of the samplesPerSymbol and the sample time, Ts.
freqOffset = 50; phaseOffset = 30; pfo = comm.PhaseFrequencyOffset(... 'FrequencyOffset',freqOffset, ... 'PhaseOffset',phaseOffset, ... 'SampleRate',samplesPerSymbol/Ts);
Set the simulated SNR to 20 dB. Since the MSK modulator generates symbols with 1 Watt of power, the signal power is 1 W or 0 dB W, which is the default value for the awgn channel signal power input.
SNR = 20;
Timing Phase, Carrier Frequency, and Carrier Phase Synchronization
Create an MSK timing synchronizer to recover symbol timing phase using a fourth-order nonlinearity method.
timeSync = comm.MSKTimingSynchronizer(... 'SamplesPerSymbol',samplesPerSymbol, ... 'ErrorUpdateGain',0.02);
Create a carrier synchronizer to recover both carrier frequency and phase. Because the MSK constellation is QPSK with a 0-degree phase offset, set the comm.CarrierSynchronizer accordingly.
phaseSync = comm.CarrierSynchronizer(... 'Modulation','QPSK', ... 'ModulationPhaseOffset','Custom', ... 'CustomPhaseOffset',0, ... 'SamplesPerSymbol',1);
Stream Processing Loop
The simulation modulates data using MSK modulation. The modulated symbols pass through the channel model, which applies timing delay, carrier frequency and phase shift, and additive white Gaussian noise. The receiver performs timing phase and carrier frequency and phase recovery. Finally, the signal symbols are demodulated and the bit error rate is calculated. The plotResultsMSKSignalRecoveryEx script generates scatter plots in this order to show these effects:
Channel impairments
Timing synchronization
Carrier synchronization
At the end of the simulation, the example displays the timing phase, frequency, and phase estimates as a function of simulation time.
for p = 1:numFrames %------------------------------------------------------ % Generate and modulate data %------------------------------------------------------ txBits = randi([0 1],samplesPerFrame,1); txSym = modem(txBits); %------------------------------------------------------ % Transmit through channel %------------------------------------------------------ % % Add timing offset rxSigTimingOff = varDelay(txSym,timingOffset*samplesPerSymbol); % % Add carrier frequency and phase offset rxSigCFO = pfo(rxSigTimingOff); % % Pass the signal through an AWGN channel rxSig = awgn(rxSigCFO,SNR); % % Save the transmitted signal for plotting plot_rx = rxSig; % %------------------------------------------------------ % Timing recovery %------------------------------------------------------ if recoverTimingPhase % Recover symbol timing phase using % fourth-order nonlinearity method [rxSym,timEst] = timeSync(rxSig); % Calculate the timing delay estimate for each sample timEst = timEst(1)/samplesPerSymbol; else % Do not apply timing recovery and % simply downsample the received signal rxSym = downsample(rxSig,samplesPerSymbol); timEst = 0; end % Save the timing synchronized received signal for plotting plot_rxTimeSync = rxSym; %------------------------------------------------------ % Carrier frequency and phase recovery %------------------------------------------------------ if recoverCarrier % The following script applies carrier frequency and % phase recovery using a second order phase-locked % loop (PLL), and removes phase ambiguity [rxSym,phEst] = phaseSync(rxSym); removePhaseAmbiguityMSKSignalRecoveryEx; freqShiftEst = mean(diff(phEst)/(Ts*2*pi)); phEst = mod(mean(phEst),360); % in degrees else freqShiftEst = 0; phEst = 0; end % Save the phase synchronized received signal for plotting plot_rxPhSync = rxSym; %------------------------------------------------------ % Demodulate the received symbols %------------------------------------------------------ rxBits = demod(rxSym); %------------------------------------------------------ % Calculate the bit error rate %------------------------------------------------------ errorStats = BERCalc(txBits,rxBits); %------------------------------------------------------ % Plot results %------------------------------------------------------ plotResultsMSKSignalRecoveryEx; end
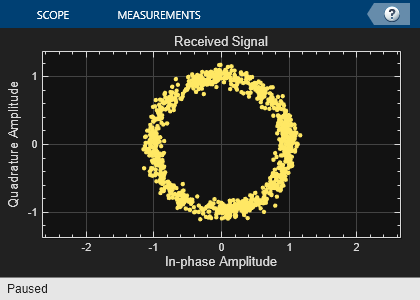
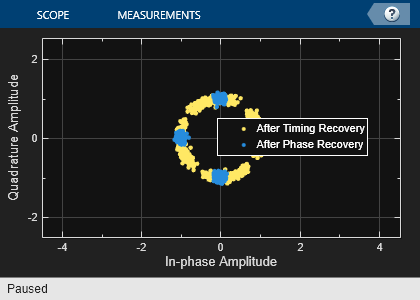
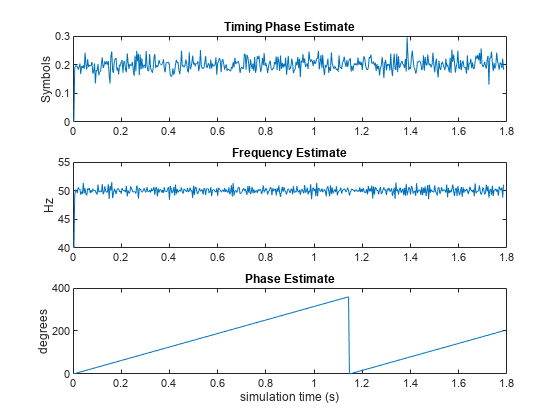
Display the bit error rate and the total number of symbols processed by the error rate calculator.
BitErrorRate = errorStats(1)
BitErrorRate = 2.0001e-06
TotalNumberOfSymbols = errorStats(3)
TotalNumberOfSymbols = 499982
Conclusion and Further Experimentation
The recovery algorithms are demonstrated by using constellation plots taken after timing, carrier frequency, and carrier phase synchronization.
Open the script to create a writable copy of this example and its supporting files. Then, to show the effects of the recovery algorithms, you can enable and disable the logical control variables recoverTimingPhase and recoverCarrier and rerun the simulation.
Appendix
This example uses these scripts:
configureMSKSignalRecoveryExplotResultsMSKSignalRecoveryExremovePhaseAmbiguityMSKSignalRecoveryEx