AnalysisPoint
Points of interest for linear analysis
Description
AnalysisPoint is a Control Design Block for marking a location
in a control system model as a point of interest for linear analysis and controller tuning.
You can combine an AnalysisPoint block with numeric LTI models, tunable LTI
models, and other Control Design Blocks to build tunable models of control systems.
AnalysisPoint locations are available for analysis with commands such as
getIOTransfer or getLoopTransfer. Such locations
are also available for specifying design goals for control system tuning.
You can combine an AnalysisPoint block with numeric LTI models, tunable
LTI models, and other Control Design Blocks to build tunable models of control systems.
AnalysisPoint locations are available for analysis with commands such as
getIOTransfer or getLoopTransfer. Such locations
are also available for specifying design goals for control system tuning.
For example, consider the following control system.
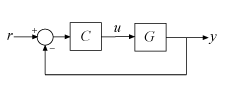
Suppose that you are interested in the effects of disturbance injected at
u in this control system. Inserting an AnalysisPoint
block at the location u associates an implied input, implied output, and
the option to open the loop at that location, as in the following diagram.
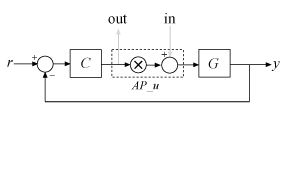
Suppose that T is a model of the control system including the
AnalysisPoint block, AP_u. In this case, the command
getIOTransfer(T,'AP_u','y') returns a model of the closed-loop transfer
function from u to y. Likewise, the command
getLoopTransfer(T,'AP_u',-1) returns a model of the negative-feedback
open-loop response, CG, measured at the location u.
AnalysisPoint blocks are also useful when tuning a control system
using tuning commands such as systune. You can use an
AnalysisPoint block to mark a loop-opening location for open-loop
tuning requirements such as TuningGoal.LoopShape or
TuningGoal.Margins. You can also use an AnalysisPoint
block to mark the specified input or output for tuning requirements such as
TuningGoal.Gain. For example, Req =
TuningGoal.Margins('AP_u',5,40) constrains the gain and phase margins at the
location u.
You can create AnalysisPoint blocks explicitly using the
AnalysisPoint command and connect them with other block diagram
components using model interconnection commands. For example, the following code creates a
model of the system illustrated above.
G = tf(1,[1 2]); C = tunablePID('C','pi'); AP_u = AnalysisPoint('u'); T = feedback(G*AP_u*C,1); % closed loop r->y
You can also create analysis points implicitly, using the connect
command. The following syntax creates a dynamic system model with analysis points, by
interconnecting multiple models sys1,sys2,...,sysN:
sys = connect(sys1,sys2,...,sysN,inputs,outputs,APs);
APs lists the signal locations at which to insert analysis points. The
software automatically creates and inserts an AnalysisPoint block with
channels corresponding to these locations. See connect for more information.
Creation
Description
AP = AnalysisPoint(name)AP anywhere in the
generalized model of your control system to mark a point of interest for linear analysis
or controller tuning. name specifies the block name.
Input Arguments
Properties
Examples
Version History
Introduced in R2014b