ss
State-space model
Description
Use ss to create real-valued or complex-valued state-space
models, or to convert dynamic system models to
state-space model form.
A state-space model is a mathematical representation of a physical system as a set of
input, output, and state variables related by first-order differential equations. The state
variables define the values of the output variables. The ss model object
can represent SISO or MIMO state-space models in continuous time or discrete time.
In continuous-time, a state-space model is of the following form:
Here, x, u and y
represent the states, inputs and outputs respectively, while A,
B, C and D are the state-space
matrices. In discrete time, a state-space model takes the form:
The ss object represents a continuous-time or discrete-time
state-space model in MATLAB® storing A, B, C and
D along with other information such as sample time, I/O names, delays,
and offsets.
You can create a state-space model object by either specifying the state, input and output
matrices directly, or by converting a model of another type (such as a transfer function model
tf) to state-space form. For more information, see State-Space Models. You
can use an ss model object to:
Perform linear analysis
Represent a linear time-invariant (LTI) model to perform control design
Combine with other LTI models to represent a more complex system
Creation
Syntax
Description
sys = ss(A,B,C,D)
For instance, consider a plant with Nx states,
Ny outputs, and Nu inputs. The state-space
matrices are:
Ais anNx-by-Nxreal- or complex-valued matrix.Bis anNx-by-Nureal- or complex-valued matrix.Cis anNy-by-Nxreal- or complex-valued matrix.Dis anNy-by-Nureal- or complex-valued matrix.
sys = ss(ltiSys,component)ss object form the measured component, the noise
component or both of specified component of an identified linear
time-invariant (LTI) model ltiSys. Use this syntax only when
ltiSys is an identified (LTI) model such as an idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox) or idgrey (System Identification Toolbox) object.
sys = ss(ssSys,'minimal')minreal(ss(sys)) where
matrix A has the smallest possible dimension.
Conversion to state-space form is not uniquely defined in the SISO case. It is also not guaranteed to produce a minimal realization in the MIMO case. For more information, see Recommended Working Representation.
sys = ss(ssSys,'explicit')ssSys. ss returns an
error if ssSys is improper. For more information on explicit
state-space realization, see State-Space Models.
Input Arguments
State matrix, specified as an Nx-by-Nx
matrix where, Nx is the number of states. This input sets the value
of property A.
Input-to-state matrix, specified as an
Nx-by-Nu matrix where, Nx
is the number of states and Nu is the number of inputs. This input
sets the value of property B.
State-to-output matrix, specified as an
Ny-by-Nx matrix where, Nx
is the number of states and Ny is the number of outputs. This input
sets the value of property C.
Feedthrough matrix, specified as an Ny-by-Nu
matrix where, Ny is the number of outputs and Nu
is the number of inputs. This input sets the value of property D.
Sample time, specified as a scalar. For more information, see Ts property.
Dynamic system to convert to state-space form, specified as a SISO or MIMO dynamic system model or array of dynamic system models. Dynamic systems that you can convert include:
Continuous-time or discrete-time numeric LTI models, such as
tf,zpk,ss, orpidmodels.Generalized or uncertain LTI models such as
genssoruss(Robust Control Toolbox) models. (Using uncertain models requires Robust Control Toolbox™ software.)The resulting state-space model assumes
current values of the tunable components for tunable control design blocks.
nominal model values for uncertain control design blocks.
Identified LTI models, such as
idtf(System Identification Toolbox),idss(System Identification Toolbox),idproc(System Identification Toolbox),idpoly(System Identification Toolbox), andidgrey(System Identification Toolbox) models. To select the component of the identified model to convert, specifycomponent. If you do not specifycomponent,ssconverts the measured component of the identified model by default. (Using identified models requires System Identification Toolbox™ software.)
Component of identified model to convert, specified as one of the following:
'measured'— Convert the measured component ofsys.'noise'— Convert the noise component ofsys'augmented'— Convert both the measured and noise components ofsys.
component only applies when sys is an
identified LTI model.
For more information on identified LTI models and their measured and noise components, see Identified LTI Models.
Dynamic system model to convert to minimal realization or explicit form, specified
as an ss model object.
Output Arguments
Output system model, returned as:
A state-space (
ss) model object, when the inputsA,B,CandDare numeric matrices or when converting from another model object type.A generalized state-space model (
genss) object, when one or more of the matricesA,B,CandDincludes tunable parameters, such asrealpparameters or generalized matrices (genmat). For an example, see Create State-Space Model with Both Fixed and Tunable Parameters.An uncertain state-space model (
uss) object, when one or more of the inputsA,B,CandDincludes uncertain matrices. Using uncertain models requires Robust Control Toolbox software.
Properties
State matrix, specified as an Nx-by-Nx matrix
where Nx is the number of states. The state-matrix can be represented
in many ways depending on the desired state-space model realization such as:
Model Canonical Form
Companion Canonical Form
Observable Canonical Form
Controllable Canonical Form
For more information, see State-Space Realizations.
Input-to-state matrix, specified as an
Nx-by-Nu matrix where Nx is
the number of states and Nu is the number of inputs.
State-to-output matrix, specified as an
Ny-by-Nx matrix where Nx is
the number of states and Ny is the number of outputs.
Feedthrough matrix, specified as an Ny-by-Nu
matrix where Ny is the number of outputs and Nu is
the number of inputs. D is also called as the static gain matrix
which represents the ratio of the output to the input under steady state
condition.
Matrix for implicit or descriptor state-space models, specified as a
Nx-by-Nx matrix. E is empty
by default, meaning that the state equation is explicit. To specify an implicit state
equation E
dx/dt = Ax +
Bu, set this property to a square matrix of the same size as
A. See dss for more information about creating
descriptor state-space models.
Since R2024a
Model offsets, specified as a structure with these fields.
| Field | Description |
|---|---|
u | Input offsets, specified as a vector of length equal to the number of inputs. |
y | Output offsets, specified as a vector of length equal to the number of outputs. |
x | State offsets, specified as a vector of length equal to the number of states. |
dx | State derivative offsets, specified as a vector of length equal to the number of states. |
For state-space model arrays, set Offsets to a structure array
with the same dimension as the model array.
When you linearize the nonlinear model
around an operating point (x0,u0), the resulting model is a state-space model with offsets:
where
For the linearization to be a good approximation of the nonlinear maps, it must
include the offsets δ0,
x0,
u0, and
y0. The linearize (Simulink Control Design) command returns both A, B,
C, D and the offsets when using the
StoreOffset option.
This property helps you manage linearization offsets and use them in operations such as response simulation, model interconnections, and model transformations.
Logical value indicating whether scaling is enabled or disabled, specified as either
0 or 1.
When Scaled is set to 0 (disabled), then most
numerical algorithms acting on the state-space model sys
automatically rescale the state vector to improve numerical accuracy. You can prevent
such auto-scaling by setting Scaled to 1
(enabled).
For more information about scaling, see prescale.
State names, specified as one of the following:
Character vector — For first-order models, for example,
'velocity'Cell array of character vectors — For models with two or more states
StateName is empty ' ' for all states by
default.
State path to facilitate state block path management in linearization, specified as one of the following:
Character vector — For first-order models
Cell array of character vectors — For models with two or more states
StatePath is empty ' ' for all states by
default.
State units, specified as one of the following:
Character vector — For first-order models, for example,
'm/s'Cell array of character vectors — For models with two or more states
Use StateUnit to keep track of the units of each state.
StateUnit has no effect on system behavior.
StateUnit is empty ' ' for all states by
default.
Internal delays in the model, specified as a vector. Internal delays arise, for example, when closing feedback loops on systems with delays, or when connecting delayed systems in series or parallel. For more information about internal delays, see Closing Feedback Loops with Time Delays.
For continuous-time models, internal delays are expressed in the time unit specified
by the TimeUnit property of the model. For discrete-time models,
internal delays are expressed as integer multiples of the sample time
Ts. For example, InternalDelay = 3 means a delay
of three sampling periods.
You can modify the values of internal delays using the property
InternalDelay. However, the number of entries in
sys.InternalDelay cannot change, because it is a structural
property of the model.
Input delay for each input channel, specified as one of the following:
Scalar — Specify the input delay for a SISO system or the same delay for all inputs of a multi-input system.
Nu-by-1 vector — Specify separate input delays for input of a multi-input system, whereNuis the number of inputs.
For continuous-time systems, specify input delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify input delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Output delay for each output channel, specified as one of the following:
Scalar — Specify the output delay for a SISO system or the same delay for all outputs of a multi-output system.
Ny-by-1 vector — Specify separate output delays for output of a multi-output system, whereNyis the number of outputs.
For continuous-time systems, specify output delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify output delays in integer multiples of the sample time, Ts.
For more information, see Time Delays in Linear Systems.
Sample time, specified as:
0for continuous-time systems.A positive scalar representing the sampling period of a discrete-time system. Specify
Tsin the time unit specified by theTimeUnitproperty.-1for a discrete-time system with an unspecified sample time.
Time variable units, specified as one of the following:
'nanoseconds''microseconds''milliseconds''seconds''minutes''hours''days''weeks''months''years'
Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.
Input channel names, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no names specified, for any input channels.
Alternatively, you can assign input names for multi-input models using automatic vector
expansion. For example, if sys is a two-input model, enter the
following.
sys.InputName = 'controls';The input names automatically expand to {'controls(1)';'controls(2)'}.
You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.
Use InputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
Input channel units, specified as one of the following:
A character vector, for single-input models.
A cell array of character vectors, for multi-input models.
'', no units specified, for any input channels.
Use InputUnit to specify input signal units. InputUnit has no effect on system behavior.
Input channel groups, specified as a structure. Use InputGroup to assign
the input channels of MIMO systems into groups and refer to each group by name. The
field names of InputGroup are the group names and the field values
are the input channels of each group. For example, enter the following to create input
groups named controls and noise that include input
channels 1 and 2, and 3 and
5, respectively.
sys.InputGroup.controls = [1 2]; sys.InputGroup.noise = [3 5];
You can then extract the subsystem from the controls inputs to all outputs
using the following.
sys(:,'controls')By default, InputGroup is a structure with no fields.
Output channel names, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no names specified, for any output channels.
Alternatively, you can assign output names for multi-output models using automatic vector
expansion. For example, if sys is a two-output model, enter the
following.
sys.OutputName = 'measurements';The output names automatically expand to {'measurements(1)';'measurements(2)'}.
You can also use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.
Use OutputName to:
Identify channels on model display and plots.
Extract subsystems of MIMO systems.
Specify connection points when interconnecting models.
Output channel units, specified as one of the following:
A character vector, for single-output models.
A cell array of character vectors, for multi-output models.
'', no units specified, for any output channels.
Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.
Output channel groups, specified as a structure. Use OutputGroup to
assign the output channels of MIMO systems into groups and refer to each group by name.
The field names of OutputGroup are the group names and the field
values are the output channels of each group. For example, create output groups named
temperature and measurement that include
output channels 1, and 3 and 5,
respectively.
sys.OutputGroup.temperature = [1]; sys.OutputGroup.measurement = [3 5];
You can then extract the subsystem from all inputs to the measurement
outputs using the following.
sys('measurement',:)By default, OutputGroup is a structure with no fields.
System name, specified as a character vector. For example, 'system_1'.
User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.
User-specified data that you want to associate with the system, specified as any MATLAB data type.
Sampling grid for model arrays, specified as a structure array.
Use SamplingGrid to track the variable values associated with each model in a model array, including identified linear time-invariant (IDLTI) model arrays.
Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.
For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.
sysarr.SamplingGrid = struct('time',0:10)Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.
[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>) M.SamplingGrid = struct('zeta',zeta,'w',w)
When you display M, each entry in the array includes the corresponding zeta and w values.
M
M(:,:,1,1) [zeta=0.3, w=5] =
25
--------------
s^2 + 3 s + 25
M(:,:,2,1) [zeta=0.35, w=5] =
25
----------------
s^2 + 3.5 s + 25
...For model arrays generated by linearizing a Simulink® model at multiple parameter values or operating points, the software populates SamplingGrid automatically with the variable values that correspond to each entry in the array. For instance, the Simulink
Control Design™ commands linearize (Simulink Control Design) and slLinearizer (Simulink Control Design) populate SamplingGrid automatically.
By default, SamplingGrid is a structure with no fields.
Object Functions
The following lists contain a representative subset of the functions you can use with
ss model objects. In general, any function applicable to Dynamic System Models is
applicable to an ss object.
step | Step response of dynamic system |
impulse | Impulse response plot of dynamic system; impulse response data |
lsim | Compute time response simulation data of dynamic system to arbitrary inputs |
bode | Bode frequency response of dynamic system |
nyquist | Nyquist response of dynamic system |
nichols | Nichols response of dynamic system |
bandwidth | Frequency response bandwidth |
Examples
Create the SISO state-space model defined by the following state-space matrices:
Specify the A, B, C and D matrices, and create the state-space model.
A = [-1.5,-2;1,0]; B = [0.5;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2
x1 -1.5 -2
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Continuous-time state-space model.
Model Properties
Create a state-space model with a sample time of 0.25 seconds and the following state-space matrices:
Specify the state-space matrices.
A = [0 1;-5 -2]; B = [0;3]; C = [0 1]; D = 0;
Specify the sample time.
Ts = 0.25;
Create the state-space model.
sys = ss(A,B,C,D,Ts);
For this example, consider a cube rotating about its corner with inertia tensor J and a damping force F of 0.2 magnitude. The input to the system is the driving torque while the angular velocities are the outputs. The state-space matrices for the cube are:
Specify the A, B, C and D matrices, and create the continuous-time state-space model.
J = [8 -3 -3; -3 8 -3; -3 -3 8]; F = 0.2*eye(3); A = -J\F; B = inv(J); C = eye(3); D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2 x3
x1 -0.04545 -0.02727 -0.02727
x2 -0.02727 -0.04545 -0.02727
x3 -0.02727 -0.02727 -0.04545
B =
u1 u2 u3
x1 0.2273 0.1364 0.1364
x2 0.1364 0.2273 0.1364
x3 0.1364 0.1364 0.2273
C =
x1 x2 x3
y1 1 0 0
y2 0 1 0
y3 0 0 1
D =
u1 u2 u3
y1 0 0 0
y2 0 0 0
y3 0 0 0
Continuous-time state-space model.
Model Properties
sys is MIMO since the system contains 3 inputs and 3 outputs observed from matrices C and D. For more information on MIMO state-space models, see MIMO State-Space Models.
Create a state-space model using the following discrete-time, multi-input, multi-output state matrices with sample time ts = 0.2 seconds:
Specify the state-space matrices and create the discrete-time MIMO state-space model.
A = [-7,0;0,-10]; B = [5,0;0,2]; C = [1,-4;-4,0.5]; D = [0,-2;2,0]; ts = 0.2; sys = ss(A,B,C,D,ts)
sys =
A =
x1 x2
x1 -7 0
x2 0 -10
B =
u1 u2
x1 5 0
x2 0 2
C =
x1 x2
y1 1 -4
y2 -4 0.5
D =
u1 u2
y1 0 -2
y2 2 0
Sample time: 0.2 seconds
Discrete-time state-space model.
Model Properties
Create state-space matrices and specify sample time.
A = [-0.2516 -0.1684;2.784 0.3549]; B = [0;3]; C = [0 1]; D = 0; Ts = 0.05;
Create the state-space model, specifying the state and input names using name-value pairs.
sys = ss(A,B,C,D,Ts,'StateName',{'Position' 'Velocity'},... 'InputName','Force');
The number of state and input names must be consistent with the dimensions of A, B, C, and D.
Naming the inputs and outputs can be useful when dealing with response plots for MIMO systems.
step(sys)
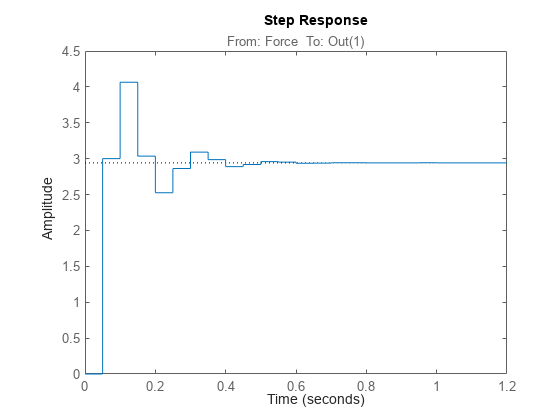
Notice the input name Force in the title of the step response plot.
For this example, create a state-space model with the same time and input unit properties inherited from another state-space model. Consider the following state-space models:
First, create a state-space model sys1 with the TimeUnit and InputUnit property set to 'minutes'.
A1 = [-1.5,-2;1,0]; B1 = [0.5;0]; C1 = [0,1]; D1 = 5; sys1 = ss(A1,B1,C1,D1,'TimeUnit','minutes','InputUnit','minutes');
Verify that the time and input unit properties of sys1 are set to 'minutes'.
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1×2 cell
{'minutes'} {'minutes'}
Create the second state-space model with properties inherited from sys1.
A2 = [7,-1;0,2]; B2 = [0.85;2]; C2 = [10,14]; D2 = 2; sys2 = ss(A2,B2,C2,D2,sys1);
Verify that the time and input units of sys2 have been inherited from sys1.
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1×2 cell
{'minutes'} {'minutes'}
In this example, you will create a static gain MIMO state-space model.
Consider the following two-input, two-output static gain matrix:
Specify the gain matrix and create the static gain state-space model.
D = [2,4;3,5]; sys1 = ss(D)
sys1 =
D =
u1 u2
y1 2 4
y2 3 5
Static gain.
Model Properties
Compute the state-space model of the following transfer function:
Create the transfer function model.
H = [tf([1 1],[1 3 3 2]) ; tf([1 0 3],[1 1 1])];
Convert this model to a state-space model.
sys = ss(H);
Examine the size of the state-space model.
size(sys)
State-space model with 2 outputs, 1 inputs, and 5 states.
The number of states is equal to the cumulative order of the SISO entries in H(s).
To obtain a minimal realization of H(s), enter
sys = ss(H,'minimal');
size(sys)State-space model with 2 outputs, 1 inputs, and 3 states.
The resulting model has an order of three, which is the minimum number of states needed to represent H(s). To see this number of states, refactor H(s) as the product of a first-order system and a second-order system.
For this example, extract the measured and noise components of an identified polynomial model into two separate state-space models.
Load the Box-Jenkins polynomial model ltiSys in identifiedModel.mat.
load('identifiedModel.mat','ltiSys');
ltiSys is an identified discrete-time model of the form: , where represents the measured component and the noise component.
Extract the measured and noise components as state-space models.
sysMeas = ss(ltiSys,'measured') sysMeas =
A =
x1 x2
x1 1.575 -0.6115
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 -0.2851 0.3916
D =
u1
y1 0
Input delays (sampling periods): 2
Sample time: 0.04 seconds
Discrete-time state-space model.
Model Properties
sysNoise = ss(ltiSys,'noise')sysNoise =
A =
x1 x2 x3
x1 1.026 -0.26 0.3899
x2 1 0 0
x3 0 0.5 0
B =
v@y1
x1 0.25
x2 0
x3 0
C =
x1 x2 x3
y1 0.319 -0.04738 0.07106
D =
v@y1
y1 0.04556
Input groups:
Name Channels
Noise 1
Sample time: 0.04 seconds
Discrete-time state-space model.
Model Properties
The measured component can serve as a plant model, while the noise component can be used as a disturbance model for control system design.
Create a descriptor state-space model (E ≠ I).
a = [2 -4; 4 2]; b = [-1; 0.5]; c = [-0.5, -2]; d = [-1]; e = [1 0; -3 0.5]; sysd = dss(a,b,c,d,e);
Compute an explicit realization of the system (E = I).
syse = ss(sysd,'explicit')syse =
A =
x1 x2
x1 2 -4
x2 20 -20
B =
u1
x1 -1
x2 -5
C =
x1 x2
y1 -0.5 -2
D =
u1
y1 -1
Continuous-time state-space model.
Model Properties
Confirm that the descriptor and explicit realizations have equivalent dynamics.
bodeplot(sysd,syse,'g--')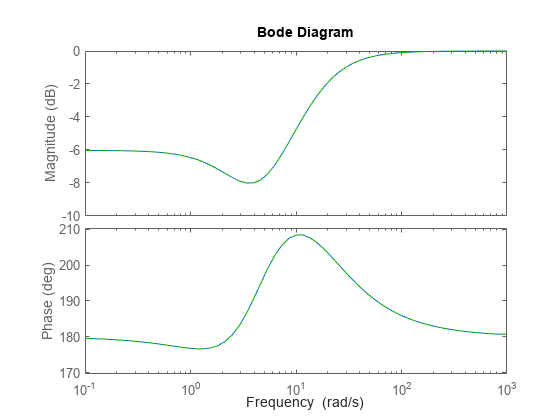
This example shows how to create a state-space genss model having both fixed and tunable parameters.
where a and b are tunable parameters, whose initial values are -1 and 3, respectively.
Create the tunable parameters using realp.
a = realp('a',-1); b = realp('b',3);
Define a generalized matrix using algebraic expressions of a and b.
A = [1 a+b;0 a*b];
A is a generalized matrix whose Blocks property contains a and b. The initial value of A is [1 2;0 -3], from the initial values of a and b.
Create the fixed-value state-space matrices.
B = [-3.0;1.5]; C = [0.3 0]; D = 0;
Use ss to create the state-space model.
sys = ss(A,B,C,D)
Generalized continuous-time state-space model with 1 outputs, 1 inputs, 2 states, and the following blocks: a: Scalar parameter, 2 occurrences. b: Scalar parameter, 2 occurrences. Model Properties Type "ss(sys)" to see the current value and "sys.Blocks" to interact with the blocks.
sys is a generalized LTI model (genss) with tunable parameters a and b.
For this example, consider a SISO state-space model defined by the following state-space matrices:
Considering an input delay of 0.5 seconds and an output delay of 2.5 seconds, create a state-space model object to represent the A, B, C and D matrices.
A = [-1.5,-2;1,0]; B = [0.5;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D,'InputDelay',0.5,'OutputDelay',2.5)
sys =
A =
x1 x2
x1 -1.5 -2
x2 1 0
B =
u1
x1 0.5
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Input delays (seconds): 0.5
Output delays (seconds): 2.5
Continuous-time state-space model.
Model Properties
You can also use the get command to display all the properties of a MATLAB object.
get(sys)
A: [2×2 double]
B: [2×1 double]
C: [0 1]
D: 0
E: []
Offsets: []
Scaled: 0
StateName: {2×1 cell}
StatePath: {2×1 cell}
StateUnit: {2×1 cell}
InternalDelay: [0×1 double]
InputDelay: 0.5000
OutputDelay: 2.5000
InputName: {''}
InputUnit: {''}
InputGroup: [1×1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ''
Ts: 0
TimeUnit: 'seconds'
SamplingGrid: [1×1 struct]
For more information on specifying time delay for an LTI model, see Specifying Time Delays.
For this example, consider a state-space System object™ that represents the following state matrices:
Create a state-space object sys using the ss command.
A = [-1.2,-1.6,0;1,0,0;0,1,0]; B = [1;0;0]; C = [0,0.5,1.3]; D = 0; sys = ss(A,B,C,D);
Next, compute the closed-loop state-space model for a unit negative gain and find the poles of the closed-loop state-space System object sysFeedback.
sysFeedback = feedback(sys,1); P = pole(sysFeedback)
P = 3×1 complex
-0.2305 + 1.3062i
-0.2305 - 1.3062i
-0.7389 + 0.0000i
The feedback loop for unit gain is stable since all poles have negative real parts. Checking the closed-loop poles provides a binary assessment of stability. In practice, it is more useful to know how robust (or fragile) stability is. One indication of robustness is how much the loop gain can change before stability is lost. You can use the root locus plot to estimate the range of k values for which the loop is stable.
rlocus(sys)
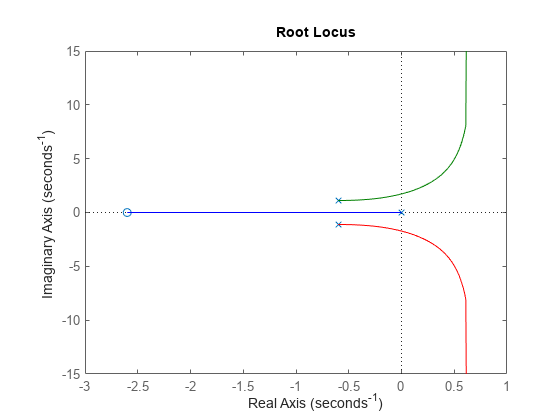
Changes in the loop gain are only one aspect of robust stability. In general, imperfect plant modeling means that both gain and phase are not known exactly. Since modeling errors have the most detrimental effect near the gain crossover frequency (frequency where open-loop gain is 0dB), it also matters how much phase variation can be tolerated at this frequency.
You can display the gain and phase margins on a Bode plot as follows.
bode(sys) grid
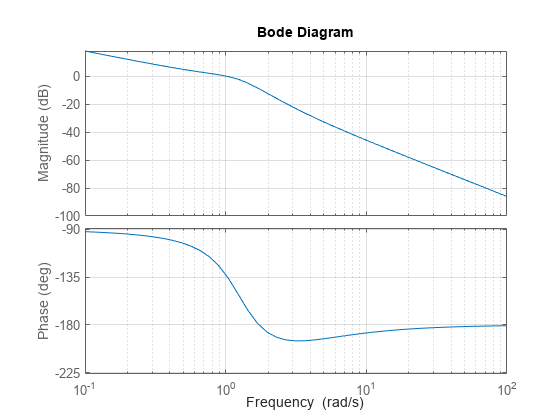
For a more detailed example, see Assessing Gain and Phase Margins.
For this example, design a 2-DOF PID controller with a target bandwidth of 0.75 rad/s for a system represented by the following matrices:
Create a state-space object sys using the ss command.
A = [-0.5,-0.1;1,0]; B = [1;0]; C = [0,1]; D = 0; sys = ss(A,B,C,D)
sys =
A =
x1 x2
x1 -0.5 -0.1
x2 1 0
B =
u1
x1 1
x2 0
C =
x1 x2
y1 0 1
D =
u1
y1 0
Continuous-time state-space model.
Model Properties
Using the target bandwidth, use pidtune to generate a 2-DOF controller.
wc = 0.75;
C2 = pidtune(sys,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 0.513, Ki = 0.0975, Kd = 0.577, b = 0.344, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Model Properties
Using the type 'PID2' causes pidtune to generate a 2-DOF controller, represented as a pid2 object. The display confirms this result. The display also shows that pidtune tunes all controller coefficients, including the setpoint weights b and c, to balance performance and robustness.
For interactive PID tuning in the Live Editor, see the Tune PID Controller Live Editor task. This task lets you interactively design a PID controller and automatically generates MATLAB code for your live script.
For interactive PID tuning in a standalone app, use PID Tuner. See PID Controller Design for Fast Reference Tracking for an example of designing a controller using the app.
Consider a state-space plant G with five inputs and four outputs and a state-space feedback controller K with three inputs and two outputs. The outputs 1, 3, and 4 of the plant G must be connected the controller K inputs, and the controller outputs to inputs 4 and 2 of the plant.
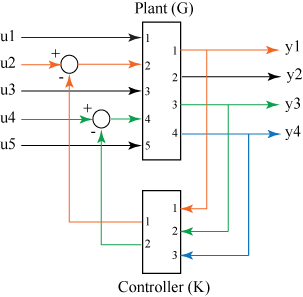
For this example, consider two continuous-time state-space models for both G and K represented by the following set of matrices:
AG = [-3,0.4,0.3;-0.5,-2.8,-0.8;0.2,0.8,-3]; BG = [0.4,0,0.3,0.2,0;-0.2,-1,0.1,-0.9,-0.5;0.6,0.9,0.5,0.2,0]; CG = [0,-0.1,-1;0,-0.2,1.6;-0.7,1.5,1.2;-1.4,-0.2,0]; DG = [0,0,0,0,-1;0,0.4,-0.7,0,0.9;0,0.3,0,0,0;0.2,0,0,0,0]; sysG = ss(AG,BG,CG,DG)
sysG =
A =
x1 x2 x3
x1 -3 0.4 0.3
x2 -0.5 -2.8 -0.8
x3 0.2 0.8 -3
B =
u1 u2 u3 u4 u5
x1 0.4 0 0.3 0.2 0
x2 -0.2 -1 0.1 -0.9 -0.5
x3 0.6 0.9 0.5 0.2 0
C =
x1 x2 x3
y1 0 -0.1 -1
y2 0 -0.2 1.6
y3 -0.7 1.5 1.2
y4 -1.4 -0.2 0
D =
u1 u2 u3 u4 u5
y1 0 0 0 0 -1
y2 0 0.4 -0.7 0 0.9
y3 0 0.3 0 0 0
y4 0.2 0 0 0 0
Continuous-time state-space model.
Model Properties
AK = [-0.2,2.1,0.7;-2.2,-0.1,-2.2;-0.4,2.3,-0.2]; BK = [-0.1,-2.1,-0.3;-0.1,0,0.6;1,0,0.8]; CK = [-1,0,0;-0.4,-0.2,0.3]; DK = [0,0,0;0,0,-1.2]; sysK = ss(AK,BK,CK,DK)
sysK =
A =
x1 x2 x3
x1 -0.2 2.1 0.7
x2 -2.2 -0.1 -2.2
x3 -0.4 2.3 -0.2
B =
u1 u2 u3
x1 -0.1 -2.1 -0.3
x2 -0.1 0 0.6
x3 1 0 0.8
C =
x1 x2 x3
y1 -1 0 0
y2 -0.4 -0.2 0.3
D =
u1 u2 u3
y1 0 0 0
y2 0 0 -1.2
Continuous-time state-space model.
Model Properties
Define the feedout and feedin vectors based on the inputs and outputs to be connected in a feedback loop.
feedin = [4 2]; feedout = [1 3 4]; sys = feedback(sysG,sysK,feedin,feedout,-1)
sys =
A =
x1 x2 x3 x4 x5 x6
x1 -3 0.4 0.3 0.2 0 0
x2 1.18 -2.56 -0.8 -1.3 -0.2 0.3
x3 -1.312 0.584 -3 0.56 0.18 -0.27
x4 2.948 -2.929 -2.42 -0.452 1.974 0.889
x5 -0.84 -0.11 0.1 -2.2 -0.1 -2.2
x6 -1.12 -0.26 -1 -0.4 2.3 -0.2
B =
u1 u2 u3 u4 u5
x1 0.4 0 0.3 0.2 0
x2 -0.44 -1 0.1 -0.9 -0.5
x3 0.816 0.9 0.5 0.2 0
x4 -0.2112 -0.63 0 0 0.1
x5 0.12 0 0 0 0.1
x6 0.16 0 0 0 -1
C =
x1 x2 x3 x4 x5 x6
y1 0 -0.1 -1 0 0 0
y2 -0.672 -0.296 1.6 0.16 0.08 -0.12
y3 -1.204 1.428 1.2 0.12 0.06 -0.09
y4 -1.4 -0.2 0 0 0 0
D =
u1 u2 u3 u4 u5
y1 0 0 0 0 -1
y2 0.096 0.4 -0.7 0 0.9
y3 0.072 0.3 0 0 0
y4 0.2 0 0 0 0
Continuous-time state-space model.
Model Properties
size(sys)
State-space model with 4 outputs, 5 inputs, and 6 states.
sys is the resultant closed loop state-space model obtained by connecting the specified inputs and outputs of G and K.
Since R2024a
This example shows how to linearize a Simulink® model and store the linearization offsets in the Offsets property of the ss model object.
Open the Simulink model.
mdl = 'watertankNLModel';
open_system(mdl)Specify the initial condition for water height.
h0 = 10;
Specify model linear analysis points.
io(1) = linio('watertankNLModel/Step',1,'input'); io(2) = linio('watertankNLModel/H',1,'output');
Simulate the model and extract operating points at time snapshots.
tlin = [0 15 30]; op = findop(mdl,tlin);
Compute the linearization result along with offsets.
options = linearizeOptions('StoreOffsets',true);
[linsys,~,info] = linearize(mdl,io,op,options);The function returns an array of state-space models linsys and their corresponding linearization offsets in info.Offsets.
The Offsets property of the ss model object requires a structure with fields u, y, x, and dx. You can use the info.Offsets output from linearize to set these offsets directly.
linsys.Offsets = info.Offsets; linsys.Offsets
ans=3×1 struct array with fields:
dx
x
u
y
Version History
Introduced before R2006aUse the new Offsets property to store model offsets. Offsets
usually arise when linearizing nonlinear dynamics at some operating conditions. This
property helps you manage linearization offsets and use them in operations such as response
simulation, model interconnections, and model transformations.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)