csaps
Cubic smoothing spline
Syntax
Description
Note
For a simpler but less flexible method to generate smoothing splines, try the Curve Fitter
app or the fit function.
pp = csaps(x,y)(x,y)
in ppform. The value of spline f at data site x(j)
approximates the data value y(:,j) for j =
1:length(x).
The smoothing spline f minimizes
Here, n is the number of entries of x and the
integral is over the smallest interval containing all the entries of x.
yj and
xj refer to the
jth entries of y and x,
respectively. D2f denotes
the second derivative of the function f.
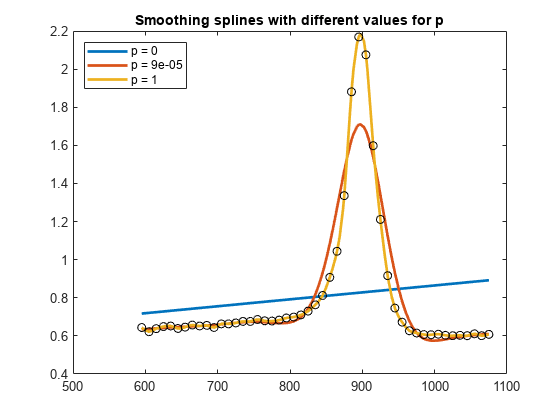
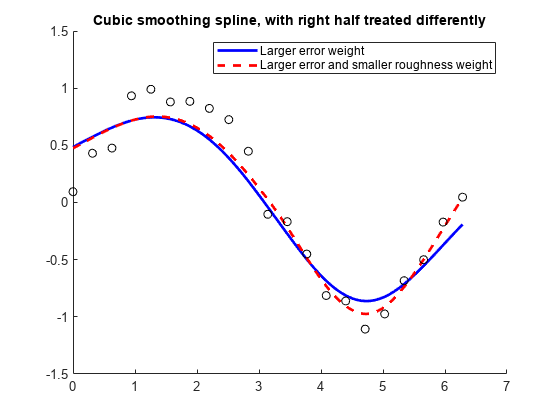
The default values for the error measure weights
wj are 1. The default value
for the piecewise constant weight function λ in the roughness measure is the constant function 1. By default,
csaps chooses a value for the smoothing parameter p based on the given data sites
x.
To evaluate a smoothing spline outside its basic interval, you must first extrapolate
it. Use the command pp = fnxtr(pp) to ensure that the second derivative
is zero outside the interval spanned by the data sites.
[___] = csaps({x1,...,xm},
provides the ppform of an y,___)m-variate tensor-product smoothing spline to
data on the rectangular grid described by {x1,...,xm}. You can use this
syntax with any of the arguments in the previous syntaxes.
Examples
Input Arguments
Output Arguments
Algorithms
csaps is an implementation of the Fortran routine
SMOOTH from PGS.
The calculation of the smoothing spline requires solving a linear system whose coefficient
matrix has the form p*A + (1-p)*B, with the matrices A
and B depending on the data sites x. The default value
of p makes p*trace(A) equal
(1-p)*trace(B).
Version History
Introduced before R2006a