road

Add road to driving scenario or road group

Syntax

road(scenario,roadcenters)

road(scenario,roadcenters,roadwidth)

road(scenario,roadcenters,roadwidth,bankingangle)

road(scenario,roadcenters,'Lanes',lspec)

road(scenario,roadcenters,bankingangle,'Lanes',lspec)

road(___,'Name',name)

rd = road(___)

road(rg,roadcenters)

road(rg,roadcenters,roadwidth)

road(rg,roadcenters,roadwidth,bankingangle)

road(rg,roadcenters,'Lanes',lspec)

road(rg,roadcenters,bankingangle,'Lanes',lspec)

road(___,'Name',name)

Description

Add Roads To Driving Scenario

road(scenario,roadcenters) adds a road to a driving scenario, scenario. You specify the road shape and the orientation of a road in the 2-D plane by using a set of road centers, roadcenters, at discrete points. When you specify the number of lanes on a road, the lanes are numbered with respect to the road centers. For more information, see Draw Direction of Road and Numbering of Lanes.

road(scenario,roadcenters,roadwidth) adds a road with the specified width, roadwidth.

road(scenario,roadcenters,roadwidth,bankingangle) adds a road with the specified width and banking angle, bankingangle.

road(scenario,roadcenters,'Lanes',lspec) adds a road with the specified lanes, lspec.

road(scenario,roadcenters,bankingangle,'Lanes',lspec) adds a road with the specified banking angle and lanes.

road(___,'Name',name) specifies the name of the road, using any of the input argument combinations from previous syntaxes.

rd = road(___) returns a Road object that stores the properties of the created road.

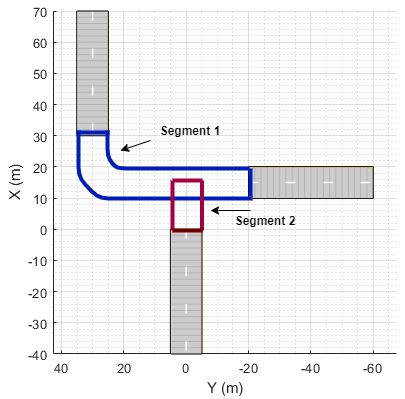
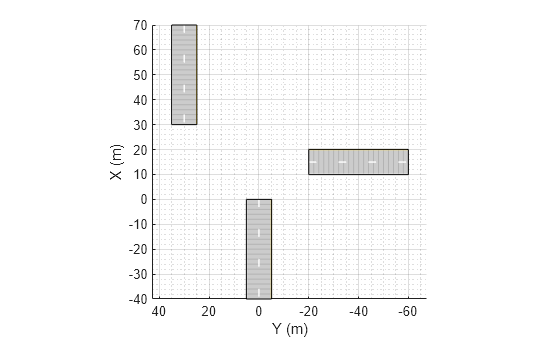
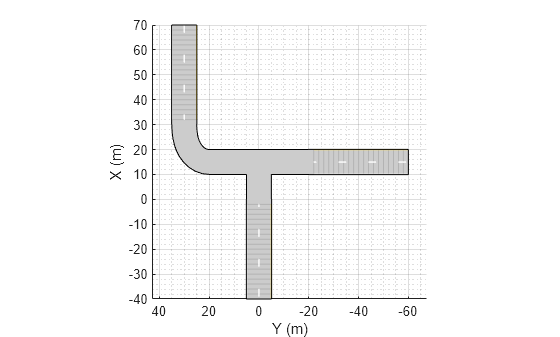
Add Roads to Road Group

road(rg,roadcenters) adds a road segment to a road group, rg. Use a road group to create a road junction or intersection. You specify the shape and the orientation of the road segment in the 2-D plane by using a set of road centers, roadcenters, at discrete points. When you specify the number of lanes on a road segment, the lanes are numbered with respect to the road centers. For more information, see Draw Direction of Road and Numbering of Lanes.

road(rg,roadcenters,roadwidth) adds a road segment with the specified width, roadwidth, to the road group.

road(rg,roadcenters,roadwidth,bankingangle) adds a road segment with the specified width and banking angle, bankingangle, to the road group.

road(rg,roadcenters,'Lanes',lspec) adds a road segment with the specified lanes, lspec, to the road group.

road(rg,roadcenters,bankingangle,'Lanes',lspec) adds a road segment with the specified banking angle and lanes to the road group.

road(___,'Name',name) specifies the name of the road segment, using any of the input argument combinations from previous syntaxes.

Examples

Create Driving Scenario with Multiple Actors and Roads

Create a driving scenario containing a curved road, two straight roads, and two actors: a car and a bicycle. Both actors move along the road for 60 seconds.

Create the driving scenario object.

scenario = drivingScenario('SampleTime',0.1','StopTime',60);

Create the curved road using road center points following the arc of a circle with an 800-meter radius. The arc starts at 0°, ends at 90°, and is sampled at 5° increments.

angs = [0:5:90]';
R = 800;
roadcenters = R*[cosd(angs) sind(angs) zeros(size(angs))];
roadwidth = 10;
road(scenario,roadcenters,roadwidth);

Add two straight roads with the default width, using road center points at each end.

roadcenters = [700 0 0; 100 0 0];
road(scenario,roadcenters)

ans = 
  Road with properties:

           Name: ""
         RoadID: 2
    RoadCenters: [2x3 double]
      RoadWidth: 6
      BankAngle: [2x1 double]

roadcenters = [400 400 0; 0 0 0];
road(scenario,roadcenters)

ans = 
  Road with properties:

           Name: ""
         RoadID: 3
    RoadCenters: [2x3 double]
      RoadWidth: 6
      BankAngle: [2x1 double]

Get the road boundaries.

rbdry = roadBoundaries(scenario);

Add a car and a bicycle to the scenario. Position the car at the beginning of the first straight road.

car = vehicle(scenario,'ClassID',1,'Position',[700 0 0], ...
    'Length',3,'Width',2,'Height',1.6);

Position the bicycle farther down the road.

bicycle = actor(scenario,'ClassID',3,'Position',[706 376 0]', ...
    'Length',2,'Width',0.45,'Height',1.5);

Plot the scenario.

plot(scenario,'Centerline','on','RoadCenters','on');
title('Scenario');

Display the actor poses and profiles.

poses = actorPoses(scenario)

poses=2×1 struct array with fields:
    ActorID
    Position
    Velocity
    Roll
    Pitch
    Yaw
    AngularVelocity

profiles = actorProfiles(scenario)

profiles=2×1 struct array with fields:
    ActorID
    ClassID
    Length
    Width
    Height
    OriginOffset
    MeshVertices
    MeshFaces
    RCSPattern
    RCSAzimuthAngles
    RCSElevationAngles

Create and Display Road Boundaries

Create a driving scenario containing a figure-8 road specified in the world coordinates of the scenario. Convert the world coordinates of the scenario to the coordinate system of the ego vehicle.

Create an empty driving scenario.

scenario = drivingScenario;

Add a figure-8 road to the scenario. Display the scenario.

roadCenters = [0  0  1
             20 -20  1
             20  20  1
            -20 -20  1
            -20  20  1
              0   0  1];

roadWidth = 3;
bankAngle = [0 15 15 -15 -15 0];
road(scenario,roadCenters,roadWidth,bankAngle);
plot(scenario)

Add an ego vehicle to the scenario. Position the vehicle at world coordinates (20, –20) and orient it at a –15 degree yaw angle.

ego = actor(scenario,'ClassID',1,'Position',[20 -20 0],'Yaw',-15);

Obtain the road boundaries in ego vehicle coordinates by using the roadBoundaries function. Specify the ego vehicle as the input argument.

rbEgo1 = roadBoundaries(ego);

Display the result on a bird's-eye plot.

bep = birdsEyePlot;
lbp = laneBoundaryPlotter(bep,'DisplayName','Road');
plotLaneBoundary(lbp,rbEgo1)

Obtain the road boundaries in world coordinates by using the roadBoundaries function. Specify the scenario as the input argument.

rbScenario = roadBoundaries(scenario);

Obtain the road boundaries in ego vehicle coordinates by using the driving.scenario.roadBoundariesToEgo function.

rbEgo2 = driving.scenario.roadBoundariesToEgo(rbScenario,ego);

Display the road boundaries on a bird's-eye plot.

bep = birdsEyePlot;
lbp = laneBoundaryPlotter(bep,'DisplayName','Road boundaries');
plotLaneBoundary(lbp,{rbEgo2})

Display Lane Markings in Car and Pedestrian Scenario

Create a driving scenario containing a car and pedestrian on a straight road. Then, create and display the lane markings of the road on a bird's-eye plot.

Create an empty driving scenario.

scenario = drivingScenario;

Create a straight, 25-meter road segment with two travel lanes in one direction.

lm = [laneMarking('Solid')
      laneMarking('Dashed','Length',2,'Space',4)
      laneMarking('Solid')];
l = lanespec(2,'Marking',lm);
road(scenario,[0 0 0; 25 0 0],'Lanes',l);

Add to the driving scenario a pedestrian crossing the road at 1 meter per second and a car following the road at 10 meters per second.

ped = actor(scenario,'ClassID',4,'Length',0.2,'Width',0.4,'Height',1.7);
car = vehicle(scenario,'ClassID',1);
smoothTrajectory(ped,[15 -3 0; 15 3 0],1);
smoothTrajectory(car,[car.RearOverhang 0 0; 25-car.Length+car.RearOverhang 0 0],10);

Display the scenario and corresponding chase plot.

plot(scenario)

chasePlot(car)

Run the simulation.

1. Create a bird's-eye plot.

2. Create an outline plotter, lane boundary plotter, and lane marking plotter for the bird's-eye plot.

3. Obtain the road boundaries and target outlines.

4. Obtain the lane marking vertices and faces.

5. Display the lane boundaries and lane markers.

6. Run the simulation loop.

bep = birdsEyePlot('XLim',[-25 25],'YLim',[-10 10]);
olPlotter = outlinePlotter(bep);
lbPlotter = laneBoundaryPlotter(bep);
lmPlotter = laneMarkingPlotter(bep,'DisplayName','Lanes');
legend('off');
while advance(scenario)
    rb = roadBoundaries(car);
    [position,yaw,length,width,originOffset,color] = targetOutlines(car);
    [lmv,lmf] = laneMarkingVertices(car);
    plotLaneBoundary(lbPlotter,rb);
    plotLaneMarking(lmPlotter,lmv,lmf);
    plotOutline(olPlotter,position,yaw,length,width, ...
        'OriginOffset',originOffset,'Color',color);
end

Create Road Network with Three-way Intersection

A three-way intersection is a Y-Junction in which two adjacent roads intersect the third road at an obtuse angle, as shown in this figure. To connect the three roads, you will create a Y-Junction by adding three road segments.

Add Three Roads to Driving Scenario

Create an empty driving scenario.

scenario = drivingScenario;

Specify the number of lanes and the width of each lane in the roads.

ls = lanespec(2,'Width',5);

Define the road centers for three roads and add them to the driving scenario. The first road is diagonally oriented to the left of the scenario canvas, second road is diagonally oriented to the right of the scenario canvas, and the third road is oriented vertically.

% Add the first road
roadCenters = [-20 0; 6 0];
road(scenario,roadCenters,'Name','Road 1','Lanes',ls);

% Add the second road
roadCenters = [23 7; 50 33];
road(scenario,roadCenters,'Name','Road 2','Lanes',ls);

% Add the third road
roadCenters = [23 -7; 50 -33];
road(scenario,roadCenters,'Name','Road 3','Lanes',ls);

Plot the scenario.

figure
plot(scenario)

Create Y-Junction to Connect Roads

Create a RoadGroup object. Specify the width for each road segment that forms the Y-junction.

rg = driving.scenario.RoadGroup('Name','Y-Junction');
roadWidth = 10;

Specify the road centers for three road segments, and add these road segments to the RoadGroup object by using the road function. These road segments intersect with each other.

% Add the first road segment
roadCenters = [23 7; 14 1; 6 0];
road(rg,roadCenters,roadWidth,'Name','Segment 1');

% Add the second road segment
roadCenters = [23 -7; 14 -1; 6 0];
road(rg,roadCenters,roadWidth,'Name','Segment 2');

% Add the third road segment
roadCenters = [23 7; 21 4; 21 -4; 23 -7];
road(rg,roadCenters,roadWidth,'Name','Segment 3');

Add Y-Junction to Driving Scenario

Add the road segments stored in the RoadGroup object to the driving scenario by using the roadGroup function. The road segments form a Y-Junction that connects the three roads in the driving scenario.

roadGroup(scenario,rg);

Input Arguments

scenario — Driving scenario

drivingScenario object

Driving scenario, specified as a drivingScenario object.

rg — Road group

RoadGroup object

Road group that defines a road junction or intersection, specified as a RoadGroup object.

roadcenters — Road centers used to define road

real-valued N-by-2 matrix | real-valued N-by-3 matrix

Road centers used to define a road, specified as a real-valued N-by-2 or N-by-3 matrix. Road centers determine the center line of the road at discrete points.

• If roadcenters is an N-by-2 matrix, then each matrix row represents the (x, y) coordinates of a road center. The z-coordinate of each road center is zero.

• If roadcenters is an N-by-3 matrix, then each matrix row represents the (x, y, z) coordinates of a road center.

If the first row of the matrix is the same as the last row, the road is a loop. Units are in meters.

Data Types: double

roadwidth — Width of road

6.0 (default) | positive real scalar | []

Width of road, specified as a positive real scalar. The width is constant along the entire road. Units are in meters.

To specify the bankingangle input but not roadwidth, specify roadwidth as an empty argument, [].

If you specify roadwidth, then you cannot specify the lspec input.

Data Types: double

bankingangle — Banking angle of road

0 (default) | real-valued N-by-1 vector

Banking angle of road, specified as a real-valued N-by-1 vector. N is the number of road centers. The banking angle is the roll angle of the road along the direction of the road. Units are in degrees.

lspec — Lane specification

lanespec object | compositeLaneSpec object

Lane specification, specified as a lanespec or compositeLaneSpec object. Use a lanespec object to create a road with a single lane specification. You can specify the number of lanes, the width of each lane, and the type of lane markings using the lanespec object. To specify the lane markings within lanespec, use the laneMarking function.

Use a compositeLaneSpec object to create a road with multiple road segments that have different lane specifications. For more details, see compositeLaneSpec.

If you specify lspec, then you cannot specify the roadwidth input.

Example: 'Lanes',lanespec(3) specifies a three-lane road with default lane widths and lane markings.

name — Name of road

"" (default) | character vector | string scalar

Name of the road, specified as a character vector or string scalar.

Example: 'Name','Road1'

Example: "Name","Road1"

Data Types: char | string

Output Arguments

rd — Output road

Road object

Output road, returned as a Road object that has the properties described in this table. With the exception of RoadID, which is a scenario-generated property, the property names correspond to the input arguments used to create the road. All properties are read-only.

Property	Value
Name	Name of road, specified as a string scalar The name input argument sets this property. Even if you specify name as a character vector, the Name property value is a string scalar.
RoadID	Identifier of road, specified as a positive integer The scenario input argument generates a unique ID for each road in the driving scenario.
RoadCenters	Road centers used to define a road, specified as a real-valued N-by-2 or N-by-3 matrix, where N is the number of road centers The roadcenters input argument sets this property.
RoadWidth	Width of road, specified as a positive real scalar The roadwidth input argument sets this property.
BankAngle	Banking angle of road, specified as an N-by-1 real-valued vector, where N is the number of road centers in the road The bankingangle input argument sets this property.

More About

Draw Direction of Road and Numbering of Lanes

To create a road by using the road function, specify the road centers as a matrix input. The function creates a directed line that traverses the road centers, starting from the coordinates in the first row of the matrix and ending at the coordinates in the last row of the matrix. The coordinates in the first two rows of the matrix specify the draw direction of the road. These coordinates correspond to the first two consecutive road centers. The draw direction is the direction in which the roads render in the scenario plot.

To create a road by using the Driving Scenario Designer app, you can either specify the Road Centers parameter or interactively draw on the Scenario Canvas. For a detailed example, see Create a Driving Scenario. In this case, the draw direction is the direction in which roads render in the Scenario Canvas.

• For a road with a top-to-bottom draw direction, the difference between the x-coordinates of the first two consecutive road centers is positive.

• For a road with a bottom-to-top draw direction, the difference between the x-coordinates of the first two consecutive road centers is negative.

• For a road with a left-to-right draw direction, the difference between the y-coordinates of the first two consecutive road centers is positive.

• For a road with a right-to-left draw direction, the difference between the y-coordinates of the first two consecutive road centers is negative.

Numbering Lanes

Lanes must be numbered from left to right, with the left edge of the road defined relative to the draw direction of the road. For a one-way road, by default, the left edge of the road is a solid yellow marking which indicates the end of the road in transverse direction (direction perpendicular to draw direction). For a two-way road, by default, both edges are marked with solid white lines.

For example, these diagrams show how the lanes are numbered in a one-way and two-way road with a draw direction from top-to-bottom.

Numbering Lanes in a One-Way Road

Numbering Lanes in a Two-Way Road

Specify the number of lanes as a positive integer for a one-way road. If you set the integer value as 3, then the road has three lanes that travel in the same direction. The lanes are numbered starting from the left edge of the road. 1, 2, 3 denote the first, second, and third lanes of the road, respectively.

Specify the number of lanes as a two-element vector of positive integer for a two-way road. If you set the vector as [1 2], then the road has three lanes: two lanes traveling in one direction and one lane traveling in the opposite direction. Because of the draw direction, the road has one left lane and two right lanes. The lanes are numbered starting from the left edge of the road. 1L denote the only left lane of the road. 1R and 2R denote the first and second right lanes of the road, respectively.

The lane specifications apply by the order in which the lanes are numbered.

Algorithms

The road function creates a road for an actor to follow in a driving scenario. You specify the road using N two-dimensional or three-dimensional waypoints. Each of the N – 1 segments between waypoints defines a curve whose curvature varies linearly with distance along the segment. The function fits a piecewise clothoid curve to the (x, y) coordinates of the waypoints by matching the curvature on both sides of the waypoint. For a nonclosed curve, the curvature at the first and last waypoint is zero. If the first and last waypoints coincide, then the curvatures before and after the endpoints are matched. The z-coordinates of the road are interpolated using a shape-preserving piecewise cubic curve.