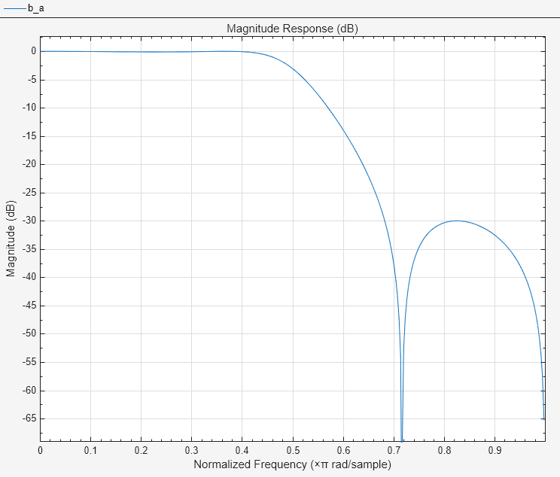
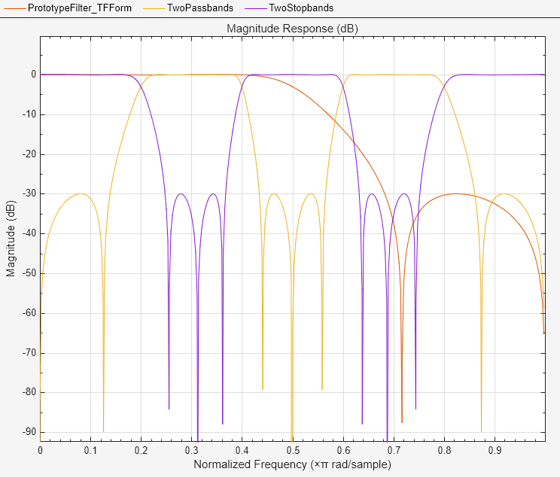
iirlp2mb
Transform IIR lowpass filter to IIR multiband filter
Syntax
Description
[
transforms an IIR lowpass filter to an IIR multiband filter.num,den,allpassNum,allpassDen] =
iirlp2mb(b,a,wo,wt)
The iirlp2mb function returns the numerator and denominator
coefficients of the transformed IIR multiband filter. The function also returns the
numerator, allpassNum, and the denominator,
allpassDen, of the
Mth order allpass mapping filter.
The prototype lowpass filter is specified with the numerator b
and the denominator a.
The function transforms a real lowpass prototype filter to a multiband filter by applying an Mth-order real lowpass to real multiple bandpass frequency mapping. Parameter M is the number of times an original feature is replicated in the transformed filter. By default the DC feature is kept at its original location. For more details, see IIR Lowpass Filter to IIR Multiband Filter Transformation.
[
allows you to specify an additional parameter, num,den,allpassNum,allpassDen] =
iirlp2mb(b,a,wo,wt,pass)pass as
'pass' or 'stop', which chooses between
using the “Nyquist Mobility” and the
“DC Mobility”, respectively. In the case of
“Nyquist Mobility”, the DC feature is kept at
an original frequency and the Nyquist feature is free to move. In the case of
“DC Mobility”, the Nyquist feature stays at
its original location and the DC feature is free to move.
Frequencies must be normalized to be between 0 and 1, with 1 corresponding to half the sample rate.
Examples
Input Arguments
Output Arguments
More About
References
[1] Franchitti, Jean-Claude. “All-pass filter interpolation and frequency transformation problems.” MSc Thesis, Dept. of Electrical and Computer Engineering, University of Colorado, 1985.
[2] Feyh, G., J.C. Franchitti and C.T. Mullis.“All-pass filter interpolation and frequency transformation problem.” Proceedings 20th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, pp. 164-168, November 1986.
[3] Mullis, C.T. and R. A. Roberts. Digital Signal Processing, section 6.7, Reading, Mass., Addison-Wesley, 1987.
[4] Feyh, G., W.B. Jones and C.T. Mullis. “An extension of the Schur Algorithm for frequency transformations.” Linear Circuits, Systems and Signal Processing: Theory and Application. C. J. Byrnes et al Eds, Amsterdam: Elsevier, 1988.
Extended Capabilities
Version History
Introduced in R2011a