Forecast Multiplicative ARIMA Model
This example shows how to forecast a multiplicative seasonal ARIMA model using forecast. The time series is monthly international airline passenger numbers from 1949 to 1960.
Load the Data and Estimate a Model.
Load the data set Data_Airline.
load Data_Airline y = log(DataTimeTable.PSSG); T = length(y); Mdl = arima('Constant',0,'D',1,'Seasonality',12,... 'MALags',1,'SMALags',12); EstMdl = estimate(Mdl,y);
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN NaN
MA{1} -0.37716 0.066794 -5.6466 1.6364e-08
SMA{12} -0.57238 0.085439 -6.6992 2.0952e-11
Variance 0.0012634 0.00012395 10.193 2.1406e-24
Forecast Airline Passenger Counts.
Use the fitted model to generate MMSE forecasts and corresponding mean square errors over a 60-month (5-year) horizon. Use the observed series as presample data. By default, forecast infers presample innovations using the specified model and observations.
[yF,yMSE] = forecast(EstMdl,60,y); upper = yF + 1.96*sqrt(yMSE); lower = yF - 1.96*sqrt(yMSE); fh = DataTimeTable.Time(end) + calmonths(1:60); figure plot(DataTimeTable.Time,y,'Color',[.75,.75,.75]) hold on h1 = plot(fh,yF,'r','LineWidth',2); h2 = plot(fh,upper,'k--','LineWidth',1.5); plot(fh,lower,'k--','LineWidth',1.5) xlim([DataTimeTable.Time(1) fh(end)]) title('Forecast and 95% Forecast Interval') legend([h1 h2],'Forecast','95% Interval','Location','NorthWest') hold off
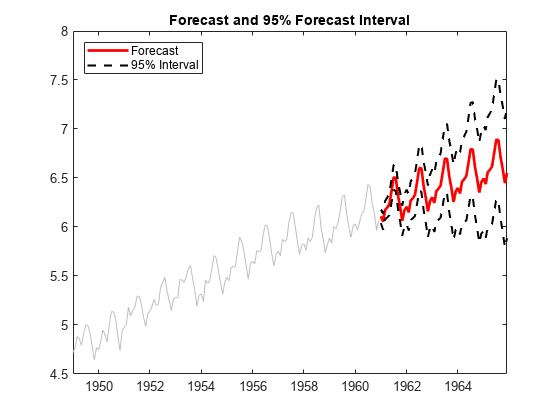
The MMSE forecast shows airline passenger counts continuing to grow over the forecast horizon. The confidence bounds show that a decline in passenger counts is plausible, however. Because this is a nonstationary process, the width of the forecast intervals grows over time.
Compare MMSE and Monte Carlo Forecasts.
Simulate 500 sample paths over the same forecast horizon. Compare the simulation mean to the MMSE forecast.
rng('default') % For reproducibility res = infer(EstMdl,y); Ysim = simulate(EstMdl,60,'NumPaths',500,'Y0',y,'E0',res); yBar = mean(Ysim,2); simU = prctile(Ysim,97.5,2); simL = prctile(Ysim,2.5,2); figure h1 = plot(fh,yF,'Color',[.85,.85,.85],'LineWidth',5); hold on h2 = plot(fh,yBar,'k--','LineWidth',1.5); plot(fh,[upper lower],'Color',[.85,.85,.85],'LineWidth',5) plot(fh,[simU simL],'k--','LineWidth',1.5) title('Comparison of MMSE and Monte Carlo Forecasts') legend([h1 h2],'MMSE','Monte Carlo','Location','NorthWest') hold off
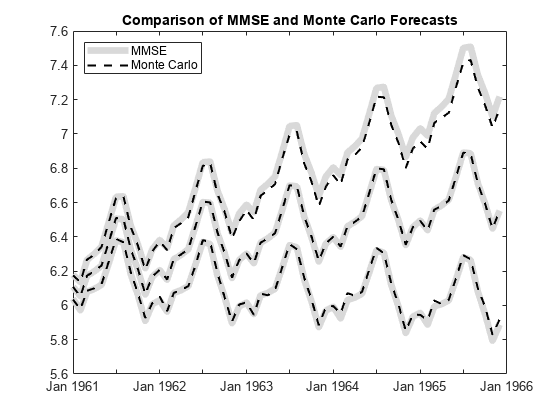
The MMSE forecast and simulation mean are virtually indistinguishable. There are slight discrepancies between the theoretical 95% forecast intervals and the simulation-based 95% forecast intervals.
See Also
Objects
Functions
Topics
- Create Multiplicative Seasonal ARIMA Model for Time Series Data
- Estimate Multiplicative ARIMA Model
- Simulate Multiplicative ARIMA Models
- Model Seasonal Lag Effects Using Indicator Variables
- Check Fit of Multiplicative ARIMA Model
- MMSE Forecasting of Conditional Mean Models
- Monte Carlo Forecasting of Conditional Mean Models