price2ret
Convert prices to returns
Syntax
Description
ReturnTbl = price2ret(PriceTbl)DataVariables name-value argument. (since R2022a)
[___] = price2ret(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)price2ret returns the output argument combination for the
corresponding input arguments. For example,
price2ret(Tbl,Method="periodic",DataVariables=1:5) computes the simple
periodic returns of the first five variables in the input table
Tbl. (since R2022a)
Examples
Load the Schwert Stock data set Data_SchwertStock.mat, which contains daily prices of the S&P index from 1930 through 2008, among other variables (enter Description for more details).
load Data_SchwertStock
numObs = height(DataTableDly)numObs = 20838
dates = datetime(datesDly,ConvertFrom="datenum");Convert the S&P price series to returns.
prices = DataTableDly.SP; returns = price2ret(prices);
returns is a 20837-by-1 vector of daily S&P returns compounded continuously.
r9 = returns(9)
r9 = 0.0033
p9_10 = [prices(9) prices(10)]
p9_10 = 1×2
21.4500 21.5200
returns(9) = 0.0033 is the daily return of the prices in the interval [21.45, 21.52].
plot(dates,DataTableDly.SP) ylabel("Price") yyaxis right plot(dates(1:end-1),returns) ylabel("Return") title("S&P Index Prices and Returns")

Since R2022a
Convert the price series in a table to simple periodic return series.
Load the US equity indices data set, which contains the table DataTable of daily closing prices of the NYSE and NASDAQ composite indices from 1990 through 2011.
load Data_EquityIdxCreate a timetable from the table.
dates = datetime(dates,ConvertFrom="datenum");
TT = table2timetable(DataTable,RowTimes=dates);
numObs = height(TT);Convert the NASDAQ and NYSE prices to simple periodic and continuously compounded returns.
varnames = ["NASDAQ" "NYSE"]; TTRetC = price2ret(TT,DataVariables=varnames); TTRetP = price2ret(TT,DataVariables=varnames,Method="periodic");
Because TT is a timetable, TTRetC and TTRetP are timetables.
Plot the return series with the corresponding prices for the last 50 observations.
idx = ((numObs - 1) - 51):(numObs - 1); figure plot(dates(idx + 1),TT.NYSE(idx + 1)) title("NYSE Index Prices and Returns") ylabel("Price") yyaxis right h = plot(dates(idx),[TTRetC.NYSE(idx) TTRetP.NYSE(idx)]); h(2).Marker = 'o'; h(2).Color = 'k'; ylabel("Return") legend(["Price" "Continuous" "Periodic"],Location="northwest") axis tight

figure plot(dates(idx + 1),TT.NASDAQ(idx + 1)) title("NASDAQ Index Prices and Returns") ylabel("Price") yyaxis right h = plot(dates(idx),[TTRetC.NASDAQ(idx) TTRetP.NASDAQ(idx)]); h(2).Marker = 'o'; h(2).Color = 'k'; ylabel("Return") legend(["Price" "Continuous" "Periodic"],Location="northwest") axis tight
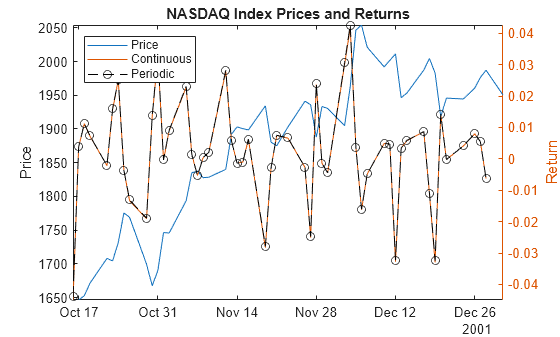
In this case, the simple periodic and continuously compounded returns of each price series are similar.
Since R2022a
Create two stock price series from continuously compounded returns that have the following characteristics:
Series 1 grows at a 10 percent rate at each observation time.
Series 2 changes at a random uniform rate in the interval [-0.1, 0.1] at each observation time.
Each series starts at price 100 and is 10 observations in length.
rng(1); % For reproducibility
numObs = 10;
p1 = 100;
r1 = 0.10;
r2 = [0; unifrnd(-0.10,0.10,numObs - 1,1)];
s1 = 100*exp(r1*(0:(numObs - 1))');
cr2 = cumsum(r2);
s2 = 100*exp(cr2);
S = [s1 s2];Convert each price series to a return series, and return the observation intervals.
[R,intervals] = price2ret(S);
Prepend the return series so that the input and output elements are of the same length and correspond.
[[NaN; intervals] S [[NaN NaN]; R] r2]
ans = 10×6
NaN 100.0000 100.0000 NaN NaN 0
1.0000 110.5171 98.3541 0.1000 -0.0166 -0.0166
1.0000 122.1403 102.7850 0.1000 0.0441 0.0441
1.0000 134.9859 93.0058 0.1000 -0.1000 -0.1000
1.0000 149.1825 89.4007 0.1000 -0.0395 -0.0395
1.0000 164.8721 83.3026 0.1000 -0.0706 -0.0706
1.0000 182.2119 76.7803 0.1000 -0.0815 -0.0815
1.0000 201.3753 72.1105 0.1000 -0.0627 -0.0627
1.0000 222.5541 69.9172 0.1000 -0.0309 -0.0309
1.0000 245.9603 68.4885 0.1000 -0.0206 -0.0206
price2ret returns rates matching the rates from the simulated series. price2ret assumes prices are recorded in a regular time base. Therefore, all durations between prices are 1.
Convert the prices to returns again, but associate the prices with years starting from August 1, 2010.
tau1 = datetime(2010,08,01); dates = tau1 + years((0:(numObs-1))'); [Ry,intervalsy] = price2ret(S,Ticks=dates); [[NaN; intervalsy] S [[NaN NaN]; Ry] r2]
ans = 10×6
NaN 100.0000 100.0000 NaN NaN 0
365.2425 110.5171 98.3541 0.0003 -0.0000 -0.0166
365.2425 122.1403 102.7850 0.0003 0.0001 0.0441
365.2425 134.9859 93.0058 0.0003 -0.0003 -0.1000
365.2425 149.1825 89.4007 0.0003 -0.0001 -0.0395
365.2425 164.8721 83.3026 0.0003 -0.0002 -0.0706
365.2425 182.2119 76.7803 0.0003 -0.0002 -0.0815
365.2425 201.3753 72.1105 0.0003 -0.0002 -0.0627
365.2425 222.5541 69.9172 0.0003 -0.0001 -0.0309
365.2425 245.9603 68.4885 0.0003 -0.0001 -0.0206
price2ret assumes time units are days. Therefore, all durations are approximately 365 and the returns are normalized for that time unit.
Compute returns again, but specify that the observation times are years.
[Ryy,intervalsyy] = price2ret(S,Ticks=dates,Units="years");
[[NaN; intervalsyy] S [[NaN NaN]; Ryy] r2]ans = 10×6
NaN 100.0000 100.0000 NaN NaN 0
1.0000 110.5171 98.3541 0.1000 -0.0166 -0.0166
1.0000 122.1403 102.7850 0.1000 0.0441 0.0441
1.0000 134.9859 93.0058 0.1000 -0.1000 -0.1000
1.0000 149.1825 89.4007 0.1000 -0.0395 -0.0395
1.0000 164.8721 83.3026 0.1000 -0.0706 -0.0706
1.0000 182.2119 76.7803 0.1000 -0.0815 -0.0815
1.0000 201.3753 72.1105 0.1000 -0.0627 -0.0627
1.0000 222.5541 69.9172 0.1000 -0.0309 -0.0309
1.0000 245.9603 68.4885 0.1000 -0.0206 -0.0206
price2ret normalizes the returns relative to years, and now the returned rates match the simulated rates.
Input Arguments
Time series of prices, specified as a
numObs-by-numVars numeric matrix. Each row of
Prices corresponds to an observation time specified by the optional
Ticks name-value argument. Each column of
Prices corresponds to an individual price series.
Data Types: double
Since R2022a
Time series of prices, specified as a table or timetable with
numObs rows. Each row of Tbl is an observation
time. For a table, the optional Ticks name-value argument specifies
observation times. For a timetable, PriceTbl.Time specifies
observation times and it must be a datetime vector.
Specify numVars variables, from which to compute returns, by
using the DataVariables argument. The selected variables must be
numeric.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: price2ret(Tbl,Method="periodic",DataVariables=1:5) computes
the simple periodic returns of the first five variables in the input table
Tbl.
Since R2022a
Observation times τ, specified as a length
numObs numeric or datetime vector of increasing values.
When the input price series are in a matrix or table, the default is
1:numObs.
When the input price series are in a timetable, price2ret
uses the row times in PriceTbl.Time and ignores
Ticks. PriceTbl.Time must be a datetime
vector.
Example: Ticks=datetime(1950:2020,12,31) specifies the end of
each year from 1950 through 2020.
Example: Ticks=datetime(1950,03,31):calquarters(1):datetime(2020,12,31)
specifies the end of each quarter during the years 1950 through 2020.
Data Types: double | datetime
Since R2022a
Time units to use when observation times Ticks are datetimes,
specified as a value in this table.
| Value | Description |
|---|---|
"milliseconds" | Milliseconds |
"seconds" | Seconds |
"minutes" | Minutes |
"hours" | Hours |
"days" | Days |
"years" | Years |
price2ret requires time units to convert duration intervals
to numeric values for normalizing returns.
When the value of the Ticks name-value argument is a numeric
vector, price2ret ignores the value of
Units.
Example: Units="years"
Data Types: char | string
Since R2022a
Compounding method, specified as a value in this table.
| Value | Description |
|---|---|
"continuous" | Compute continuously compounded returns |
"periodic" | Compute simple periodic returns |
Example: Method="periodic"
Data Types: char | string
Since R2022a
Variables in PriceTbl, from which
price2ret computes returns, specified as a string vector or
cell vector of character vectors containing variable names in
PriceTbl.Properties.VariableNames, or an integer or logical
vector representing the indices of names. The selected variables must be
numeric.
Example: DataVariables=["GDP" "CPI"]
Example: DataVariables=[true true false false] or
DataVariables=[1 2] selects the first and second table
variables.
Data Types: double | logical | char | cell | string
Output Arguments
Return series, returned as a (numObs –
1)-by-numVars numeric matrix. price2ret
returns Returns when you supply the input
Prices.
Returns in row i
ri are associated with price interval
[pi,pi+1],
i = 1:(numObs - 1), according to the compounding
method Method:
When
Methodis"continuous",When
Methodis"periodic",
When observation times τ (see
Ticks) are datetimes, the magnitude of the normalizing interval
τi+1 –
τi depends on the specified time units
(see Units).
Since R2022a
Return series and time intervals, returned as a table or timetable, the same data
type as PriceTbl, with numObs – 1 rows.
price2ret returns ReturnTbl when you
supply the input PriceTbl.
ReturnTbl contains the outputs Returns and
intervals.
ReturnTbl associates observation time
τi+1 with the end of
the interval for the returns in row i
ri.
Algorithms
Consider the following variables:
The following figure shows how the inputs and outputs are associated.

Version History
Introduced before R2006aWhen you use the optional positional inputs of price2ret to
specify observation times and the compounding method, MATLAB® issues an error stating that the syntaxes are removed. To avoid the error,
replace the optional positional inputs by using the Name=Value argument
syntax.
This syntax specifies optional positional inputs and issues an error.
price2ret(Prices,ticktimes,method)
price2ret(Prices,Ticks=ticktimes,Method=method)
When you use the optional positional inputs of price2ret to
specify observation times and the compounding method, MATLAB issues a warning stating that the syntax will be removed. To avoid the
warning, replace the optional positional inputs by using the Name=Value
argument syntax.
This syntax specifies optional positional inputs and issues a warning.
price2ret(Prices,ticktimes,method)
price2ret(Prices,Ticks=ticktimes,Method=method)
The optional positional inputs of price2ret that specify
observation times and the compounding method will be removed. To replace the optional
positional inputs, use the Name=Value argument syntax.
This syntax specifies optional positional inputs and is being removed.
price2ret(Prices,ticktimes,method)
price2ret(Prices,Ticks=ticktimes,Method=method)
Instead of using the optional positional inputs of price2ret to
specify the observation times and compounding method, use the Name=Value
argument syntax.
This syntax specifies the optional positional inputs before R2022a.
price2ret(Prices,ticktimes,method)
This syntax is the recommended replacement for R2022a and later releases.
price2ret(Prices,Ticks=ticktimes,Method=method)
In addition to accepting input data in numeric arrays, price2ret accepts input data in tables and timetables. When you supply data in a table or timetable, the following conditions apply:
price2retchooses default series on which to operate, but you can use theDataVariablesname-value argument to select variables.price2retreturns results in tables or timetables.
To convert duration intervals to numeric values for normalizing returns,
price2ret enables you to specify time units of the observation
datetimes in Ticks by using the Units name-value
argument.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)