Simulate Conditional Mean and Variance Models
This example shows how to simulate responses and conditional variances from a composite conditional mean and variance model.
Load Data and Fit Model
Load the NASDAQ data included with the toolbox. Fit a conditional mean and variance model to the daily returns. Scale the returns to percentage returns for numerical stability
load Data_EquityIdx nasdaq = DataTable.NASDAQ; r = 100*price2ret(nasdaq); T = length(r); Mdl = arima('ARLags',1,'Variance',garch(1,1),... 'Distribution','t'); EstMdl = estimate(Mdl,r,'Variance0',{'Constant0',0.001});
ARIMA(1,0,0) Model (t Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.093488 0.016694 5.6002 2.1413e-08
AR{1} 0.13911 0.018857 7.3771 1.6175e-13
DoF 7.4775 0.88261 8.472 2.4125e-17
GARCH(1,1) Conditional Variance Model (t Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.011246 0.0036305 3.0976 0.0019511
GARCH{1} 0.90766 0.010516 86.315 0
ARCH{1} 0.089897 0.010835 8.2966 1.0712e-16
DoF 7.4775 0.88261 8.472 2.4125e-17
[e0,v0] = infer(EstMdl,r);
Simulate Returns, Innovations, and Conditional Variances
Use simulate to generate 100 sample paths for the returns, innovations, and conditional variances for a 1000-period future horizon. Use the observed returns and inferred residuals and conditional variances as presample data.
rng 'default'; [y,e,v] = simulate(EstMdl,1000,'NumPaths',100,... 'Y0',r,'E0',e0,'V0',v0); figure plot(r) hold on plot(T+1:T+1000,y) xlim([0,T+1000]) title('Simulated Returns') hold off

The simulation shows increased volatility over the forecast horizon.
Plot Conditional Variances
Plot the inferred and simulated conditional variances.
figure plot(v0) hold on plot(T+1:T+1000,v) xlim([0,T+1000]) title('Simulated Conditional Variances') hold off
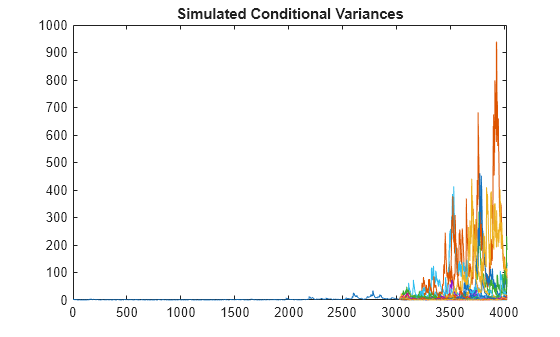
The increased volatility in the simulated returns is due to larger conditional variances over the forecast horizon.
Plot Standardized Innovations
Standardize the innovations using the square root of the conditional variance process. Plot the standardized innovations over the forecast horizon.
figure
plot(e./sqrt(v))
xlim([0,1000])
title('Simulated Standardized Innovations')
The fitted model assumes the standardized innovations follow a standardized Student's distribution. Thus, simulate generates more innovations at the distribution tails than is expected from a Gaussian data-generating process.
See Also
arima | estimate | infer | simulate
Topics
- Specify Conditional Mean and Variance Models
- Estimate Conditional Mean and Variance Model
- Forecast Conditional Mean and Variance Model
- Volatility Modeling for Soft Commodities
- Monte Carlo Simulation of Conditional Mean Models
- Presample Data for Conditional Mean Model Simulation
- Monte Carlo Forecasting of Conditional Mean Models