Smooth Time-Varying Diffuse State-Space Model
This example shows how to generate data from a known model, fit a diffuse state-space model to the data, and then smooth the states.
Suppose that a latent process comprises an AR(2) and an MA(1) model. There are 50 periods, and the MA(1) process drops out of the model for the final 25 periods. Consequently, the state equation for the first 25 periods is
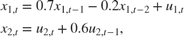
and for the last 25 periods, it is

where 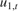 and
and 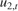 are Gaussian with mean 0 and standard deviation 1.
are Gaussian with mean 0 and standard deviation 1.
Assuming that the series starts at 1.5 and 1, respectively, generate a random series of 50 observations from  and
and 
T = 50; ARMdl = arima('AR',{0.7,-0.2},'Constant',0,'Variance',1); MAMdl = arima('MA',0.6,'Constant',0,'Variance',1); x0 = [1.5 1; 1.5 1]; rng(1); x = [simulate(ARMdl,T,'Y0',x0(:,1)),... [simulate(MAMdl,T/2,'Y0',x0(:,2));nan(T/2,1)]];
The last 25 values for the simulated MA(1) data are NaN values.
The latent processes are measured using
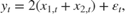
for the first 25 periods, and
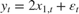
for the last 25 periods, where  is Gaussian with mean 0 and standard deviation 1.
is Gaussian with mean 0 and standard deviation 1.
Use the random latent state process (x) and the observation equation to generate observations.
y = 2*sum(x','omitnan')'+randn(T,1);
Together, the latent process and observation equations make up a state-space model. If the coefficients are unknown parameters, the state-space model is
![$$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{x_{1,t}}}\\ {{x_{2,t}}}\\ {{x_{3,t}}}\\ {{x_{4,t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _2}}&0&0\\ 1&0&0&0\\ 0&0&0&{{\theta _1}}\\ 0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{1,t - 1}}}\\ {{x_{2,t - 1}}}\\ {{x_{3,t - 1}}}\\ {{x_{4,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&0\\ 0&1\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_{1,t}}}\\ {{u_{2,t}}} \end{array}} \right]\\ {y_t} = a({x_{1,t}} + {x_{3,t}}) + {\varepsilon _t} \end{array}$$](../examples/econ/win64/SmoothTimeVaryingDiffuseStateSpaceModelExample_eq08939596656225341196.png)
for the first 25 periods,
![$$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{x_{1,t}}}\\ {{x_{2,t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _2}}&0&0\\ 1&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{1,t - 1}}}\\ {{x_{2,t - 1}}}\\ {{x_{3,t - 1}}}\\ {{x_{4,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]{u_{1,t}}\\ {y_t} = b{x_{1,t}} + {\varepsilon _t} \end{array}$$](../examples/econ/win64/SmoothTimeVaryingDiffuseStateSpaceModelExample_eq14434019549381870163.png)
for period 26, and
![$$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{x_{1,t}}}\\ {{x_{2,t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _2}}\\ 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{1,t - 1}}}\\ {{x_{2,t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]{u_{1,t}}\\ {y_t} = b{x_{1,t}} + {\varepsilon _t} \end{array}$$](../examples/econ/win64/SmoothTimeVaryingDiffuseStateSpaceModelExample_eq14967989555778478098.png)
for the last 24 periods.
Write a function that specifies how the parameters in params map to the state-space model matrices, the initial state values, and the type of state.
% Copyright 2015 The MathWorks, Inc. function [A,B,C,D,Mean0,Cov0,StateType] = diffuseAR2MAParamMap(params,T) %diffuseAR2MAParamMap Time-variant diffuse state-space model parameter %mapping function % % This function maps the vector params to the state-space matrices (A, B, % C, and D) and the type of state (StateType). From periods 1 to T/2, the % state model is an AR(2) and an MA(1) model, and the observation model is % the sum of the two states. From periods T/2 + 1 to T, the state model is % just the AR(2) model. The AR(2) model is diffuse. A1 = {[params(1) params(2) 0 0; 1 0 0 0; 0 0 0 params(3); 0 0 0 0]}; B1 = {[1 0; 0 0; 0 1; 0 1]}; C1 = {params(4)*[1 0 1 0]}; Mean0 = []; Cov0 = []; StateType = [2 2 0 0]; A2 = {[params(1) params(2) 0 0; 1 0 0 0]}; B2 = {[1; 0]}; A3 = {[params(1) params(2); 1 0]}; B3 = {[1; 0]}; C3 = {params(5)*[1 0]}; A = [repmat(A1,T/2,1);A2;repmat(A3,(T-2)/2,1)]; B = [repmat(B1,T/2,1);B2;repmat(B3,(T-2)/2,1)]; C = [repmat(C1,T/2,1);repmat(C3,T/2,1)]; D = 1; end
Save this code as a file named diffuseAR2MAParamMap on your MATLAB® path.
Create the diffuse state-space model by passing the function diffuseAR2MAParamMap as a function handle to dssm.
Mdl = dssm(@(params)diffuseAR2MAParamMap(params,T));
dssm implicitly creates the diffuse state-space model. Usually, you cannot verify diffuse state-space models that are implicitly created.
To estimate the parameters, pass the observed responses (y) to estimate. Specify an arbitrary set of positive initial values for the unknown parameters.
params0 = 0.1*ones(5,1); EstMdl = estimate(Mdl,y,params0);
Method: Maximum likelihood (fminunc)
Effective Sample size: 48
Logarithmic likelihood: -110.313
Akaike info criterion: 230.626
Bayesian info criterion: 240.186
| Coeff Std Err t Stat Prob
---------------------------------------------------
c(1) | 0.44041 0.27687 1.59069 0.11168
c(2) | 0.03949 0.29585 0.13349 0.89380
c(3) | 0.78364 1.49222 0.52515 0.59948
c(4) | 1.64260 0.66736 2.46134 0.01384
c(5) | 1.90409 0.49374 3.85648 0.00012
|
| Final State Std Dev t Stat Prob
x(1) | -0.81932 0.46706 -1.75420 0.07940
x(2) | -0.29909 0.45939 -0.65107 0.51500
EstMdl is a dssm model containing the estimated coefficients. Likelihood surfaces of state-space models might contain local maxima. Therefore, try several initial parameter values, or consider using refine.
Smooth the states and obtain the smoothed state covariance matrix per period by passing EstMdl and the observed responses to smooth.
[~,~,Output]= smooth(EstMdl,y);
Output is a T-by-1 structure array that contains the smoothed states.
Convert Output to a table.
OutputTbl = struct2table(Output);
OutputTbl(1:10,1:4) % Display first ten rows of first four variables
ans =
10×4 table
LogLikelihood SmoothedStates SmoothedStatesCov SmoothedStateDisturb
_____________ ______________ _________________ ____________________
{0×0 double} {0×0 double} {0×0 double} {0×0 double}
{0×0 double} {0×0 double} {0×0 double} {0×0 double}
{[ -2.3218]} {4×1 double} {4×4 double} {2×1 double}
{[ -2.4464]} {4×1 double} {4×4 double} {2×1 double}
{[ -3.8758]} {4×1 double} {4×4 double} {2×1 double}
{[ -2.5212]} {4×1 double} {4×4 double} {2×1 double}
{[ -1.9016]} {4×1 double} {4×4 double} {2×1 double}
{[ -1.9284]} {4×1 double} {4×4 double} {2×1 double}
{[ -2.4110]} {4×1 double} {4×4 double} {2×1 double}
{[ -2.6502]} {4×1 double} {4×4 double} {2×1 double}
The first two rows of the table contain empty cells or zeros, which correspond to the observations required to initialize the diffuse Kalman filter. That is, SwitchTime is 2.
SwitchTime = 2;
Extract the smoothed states from Output, and compute their 95% individual, Wald-type confidence intervals. Recall that the two different states are in positions 1 and 3. The states in positions 2 and 4 help to specify the processes of interest.
stateIdx = [1 3]; % State indices of interest SmoothedStates = nan(T,numel(stateIdx)); CI = nan(T,2,numel(stateIdx)); for t = (SwitchTime + 1):T maxInd = size(Output(t).SmoothedStates,1); mask = stateIdx <= maxInd; SmoothedStates(t,mask) = Output(t).SmoothedStates(stateIdx(mask),1); CovX = Output(t).SmoothedStatesCov(stateIdx(mask),stateIdx(mask)); CI(t,:,1) = SmoothedStates(t,1) + 1.96*sqrt(CovX(1,1))*[-1 1]; if (max(stateIdx(mask)) > 1) CI(t,:,2) = SmoothedStates(t,2) + 1.96*sqrt(CovX(2,2))*[-1 1]; end end SmoothedStates(1:SwitchTime,:) = 0; CI(1:SwitchTime,:,:) = 0;
Plot the true state values, the smoothed states, and the 95% smoothed-state confidence intervals for each model.
figure plot(1:T,x(:,1),'b',1:T,SmoothedStates(:,1),'k',1:T,CI(:,:,1),'--r'); title('AR(2) State Values') xlabel('Period') ylabel('State Value') legend({'True state values','Smoothed state values','95% CI'}); figure plot(1:T,x(:,2),'b',1:T,SmoothedStates(:,2),'k',1:T,CI(:,:,2),'--r'); title('MA(1) State Values') xlabel('Period') ylabel('State Value') legend({'True state values','Smoothed state values','95% CI'});


See Also
Objects
Functions
Topics
- Create Continuous State-Space Models for Economic Data Analysis
- What Is the Kalman Filter?
- Implicitly Create Time-Varying Diffuse State-Space Model
- Implicitly Create Diffuse State-Space Model Containing Regression Component
- Estimate Time-Varying Diffuse State-Space Model
- Filter Time-Varying Diffuse State-Space Model