FIS Trees
As the number of inputs to a fuzzy system increases, the number of rules increases exponentially. This large rule base reduces the computational efficiency of the fuzzy system. It also makes the operation of the fuzzy system harder to understand, and it makes the tuning of rule and membership function parameters more difficult. Because many applications have a limited amounts of training data, a large rule base reduces the generalizability of tuned fuzzy systems.
To overcome this issue, you can implement a fuzzy inference system (FIS) as a tree of smaller interconnected FIS objects rather than as a single monolithic FIS object. These FIS trees are also known as hierarchical fuzzy systems because the fuzzy systems are arranged in hierarchical tree structures. In a tree structure, the outputs of the low-level fuzzy systems are used as inputs to the high-level fuzzy systems. A FIS tree is more computationally efficient and easier to understand than a single FIS with the same number of inputs.
You can create a FIS tree using:
A
fistreeobject.The Fuzzy Logic Designer app. For an example, see Build FIS Tree Using Fuzzy Logic Designer.
Types of Hierarchical Structures
There are several FIS tree structures that you can use for your application. The following figure shows commonly used FIS tree structures: an incremental, aggregated, or cascaded structure.

Incremental Structure
In an incremental structure, input values are incorporated in multiple stages to refine the output values in several levels. For example, the previous figure shows a three-level incremental FIS tree having fuzzy inference systems , where i indicates the index of a FIS in the nth level. In an incremental FIS tree, i = 1, meaning that each level has only one fuzzy inference system. In the previous figure, the jth input of the ith FIS in the nth level is shown as input , whereas the kth output of the ith FIS in the nth level is shown as input . In the figure, n = 3, j = 1 or 2, and k = 1. If each input has m membership functions (MFs), each FIS has a complete set of m2 rules. Hence, the total number of rules is nm2 = 3 × 32 = 27.
The following figure shows a monolithic (n = 1) FIS with four inputs (j=1, 2, 3, 4) and three MFs (m = 3).

In the FIS of this figure, the total number of rules is nm4 = 1 × 34 = 81. Hence, the total number of rules in an incremental FIS tree is linear with the number of input pairs.
Input selection at different levels in an incremental FIS tree uses input rankings based on their contributions to the final output values. The input values that contribute the most are generally used at the lowest level, while the least influential ones are used at the highest level. In other words, low-rank input values are dependent on high-rank input values.
In an incremental FIS tree, each input value usually contributes to the inference process to a certain extent, without being significantly correlated with the other inputs. For example, a fuzzy system forecasts the possibility of buying an automobile using four inputs: color, number of doors, horse power, and autopilot. The inputs are four distinct automobile features, which can independently influence a buyer’s decision. Hence, the inputs can be ranked using the existing data to construct a FIS tree, as shown in the following figure.

For an example that illustrates creating an incremental FIS tree in MATLAB®, see the "Create Incremental FIS Tree" example on the fistree reference page.
Aggregated Structure
In an aggregated structure, input values are incorporated as groups at the lowest level, where each input group is fed into a FIS. The outputs of the lower level fuzzy systems are combined (aggregated) using the higher level fuzzy systems. For example, the following shows a two-level aggregated FIS tree having fuzzy inference systems , where in indicates the index of a FIS in the nth level.

In this aggregated FIS tree, i1 = 1,2 and i2 = 1. Hence, each level includes a different number of FIS. The jth input of the inth FIS is shown in the figure as input , and the kth output of the inth FIS is shown as output . In the figure, j = 1,2 and k = 1. In other words, each FIS has two inputs and one output. If each input has m MFs, then each FIS has a complete set of m2 rules. Hence, the total number of rules for the three fuzzy systems is 3 m2 = 3 × 32 = 27, which is the same as an incremental FIS for a similar configuration.
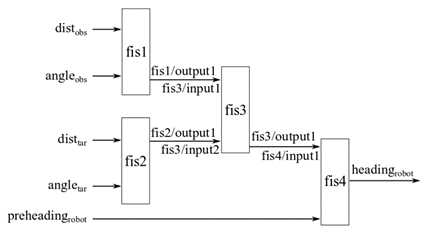
In an aggregated FIS tree, input values are naturally grouped together for specific decision-making. For example, an autonomous robot navigation task combines obstacle avoidance and target reaching subtasks for collision-free navigation. To achieve the navigation task, the FIS tree can use four inputs: distance to the closest obstacle, angle of the closest obstacle, distance to the target, and angle of the target. Distances and angles are measured with respect to the current position and heading direction of the robot. In this case, at the lowest level, the inputs naturally group as shown in the following figure: obstacle distance and obstacle angle (group 1) and target distance and target angle (group 2). Two fuzzy systems separately process individual group inputs and then another fuzzy system combines their outputs to produce a collision-free heading for the robot.

For an example that illustrates creating an aggregated FIS tree in MATLAB, see the "Create Aggregated FIS Tree" example on the fistree reference page.
Variation on Aggregated Structure
In a variation of the aggregated structure known as parallel
structure
[1], the outputs of the
lowest-level fuzzy systems are directly summed to generate the final output value. The
following figure shows an example of a parallel FIS tree, where outputs of
fis1 and fis2 are summed to produce the final
output.
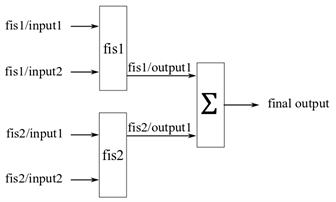
The fistree object does not provide the summing node Σ. Therefore,
you must add a custom aggregation method to evaluate a parallel FIS tree. For an example,
see the "Create and Evaluate Parallel FIS Tree" example on the fistree reference page.
Cascaded or Combined Structure
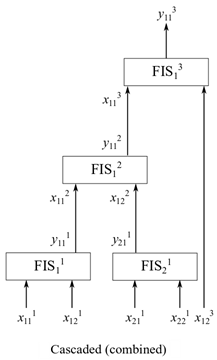
A cascaded structure, also known as combined structure, combines both incremental and aggregated structures to construct a FIS tree. This structure is suitable for a system that includes both correlated and uncorrelated inputs. The tree groups the correlated inputs in an aggregated structure, and adds uncorrelated inputs in an incremental structure. The following figure shows an example of a cascaded tree structure, where the first four inputs are grouped pairwise in an aggregated structure and the fifth input is added in an incremental structure.
For example, consider the robot navigation task discussed in Aggregated Structure. Suppose that task includes another input, the previous heading of the robot, taken into account to prevent large changes in the robot heading. You can add this input using the incremental structure of the following diagram.
For an example that illustrates creating an aggregated FIS tree in MATLAB, see the "Create Cascaded FIS Tree" example on the fistree reference page.
Add or Remove FIS Tree Outputs
When you evaluate a fistree object, it returns results for only the
open outputs, which are not connected to any FIS inputs in the FIS tree. You can optionally
access other outputs in the tree. For instance, in the following diagram of an aggregated
FIS tree, you might want to obtain the output of fis2 when you evaluate the tree.

You can add such outputs to a fistree object. You can also remove
outputs, provided that the FIS tree always has at least one output. For an example, see the
"Update FIS Tree Outputs" example on the fistree reference page.
Use the Same Value for Multiple Inputs of FIS Tree
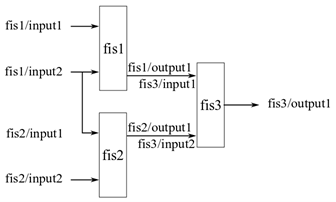
A fistree object allows using the same value for multiple inputs. For
instance, in the following figure, input2 of fis1 and
input1 of fis2 use the same value during
evaluation.
For an example showing how to construct a FIS tree in this way, see the "Use Same Value
for Multiple Inputs of a FIS Tree" example on the fistree reference page.
Update Fuzzy Inference Systems in FIS Tree
You can add or remove individual FIS elements from a fistree object.
When you do so, the software automatically updates the Connections,
Inputs, and Outputs properties of the
fistree object. For an example, see the "Update Fuzzy Inference Systems
in a FIS Tree" example on the fistree reference page.
Tune a FIS tree
Once you have configured the internal connections in your FIS tree, the next step is to tune the parameters of the tree. For an example, see Tune FIS Tree at the Command Line.
References
[1] Siddique, Nazmul, and Hojjat Adeli. Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing. Oxford, UK: John Wiley & Sons Ltd, 2013. https://doi.org/10.1002/9781118534823.