Effects of Genetic Algorithm Options
This example shows the effects of some options for the genetic algorithm function ga. You create and change options by using the optimoptions function.
Set Up a Problem for ga
ga searches for a minimum of a function using the genetic algorithm. For this example, use ga to minimize the fitness function shufcn, a real-valued function of two variables.
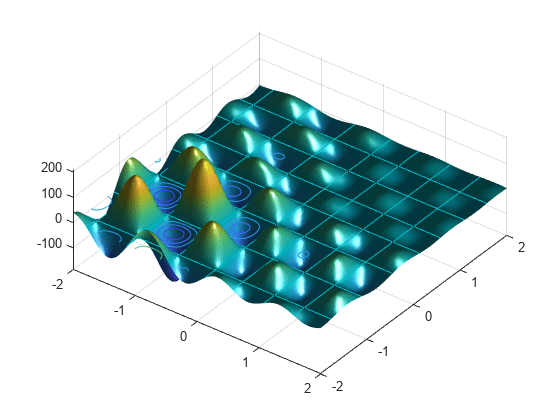
Plot shufcn over the range = [-2 2;-2 2] by calling plotobjective, which is included when you run this example.
plotobjective(@shufcn,[-2 2; -2 2]);
To use the ga solver, provide at least two input arguments: a fitness function and the number of variables in the problem. The first two output arguments returned by ga are x, the best point found, and Fval, the function value at the best point. A third output argument, exitFlag, indicates why ga stopped. ga can also return a fourth argument, Output, which contains information about the performance of the solver.
FitnessFunction = @shufcn; numberOfVariables = 2;
Run the ga solver.
rng default % For reproducibility [x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The number of generations is: %d\n', Output.generations);The number of generations is: 124
fprintf('The number of function evaluations is: %d\n', Output.funccount);The number of function evaluations is: 5881
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.199
If you run this example without the rng default command, your results can differ, because ga is a stochastic algorithm.
How the Genetic Algorithm Works
The genetic algorithm works on a population using a set of operators that are applied to the population. A population is a set of points in the design space. The initial population is generated randomly by default. The algorithm computes the next generation of the population using the fitness of the individuals in the current generation. For details, see How the Genetic Algorithm Works.
Add Visualization
To visualize the solver performance while it is running, set a 'PlotFcn' option using optimoptions. In this case, select two plot functions in a cell array. Set gaplotbestf, which plots the best and mean score of the population at every generation. Also set gaplotstopping, which plots the percentage of stopping criteria satisfied.
opts = optimoptions(@ga,'PlotFcn',{@gaplotbestf,@gaplotstopping});Run the ga solver, including the opts argument.
[x,Fval,exitFlag,Output] = ...
ga(FitnessFunction,numberOfVariables,[],[],[],[],[],[],[],opts);ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

Specify Population Options
Population options can have a large effect on solver performance. The speed of each iteration depends on the population size: a larger population leads to slower iterations. Conversely, a larger population leads to ga exploring more thoroughly, so can lead to a better solution. Similarly, a wider initial range can lead to more thorough exploration, but can require a larger population to explore the wider range with a similar thoroughness.
Specify Population Size
ga creates a default initial population by using a uniform random number generator. The default population size used by ga is 50 when the number of decision variables is less than 5, and 200 otherwise. The default size might not work well for some problems; for example, a smaller population size can be sufficient for smaller problems. Since the current problem has only two variables, specify a population size of 10. Set the value of the option PopulationSize to 10 in the existing options, opts.
opts.PopulationSize = 10;
Specify Initial Population Range
The default method for generating an initial population uses a uniform random number generator. For problems without integer constraints, ga creates an initial population where all the points are in the range –10 to 10. For example, you can generate a population of size three in the default range using this command:
Population = [-10,-10] + 20*rand(3,2);
You can set the initial range by changing the InitialPopulationRange option. The range must be a matrix with two rows. If the range has only one column, that is, it is 2-by-1, then the range of every variable is the given range. For example, if you set the range to [-1; 1], then the initial range for both variables is –1 to 1. To specify a different initial range for each variable, you must specify the range as a matrix with two rows and numberOfVariables columns. For example, if you set the range to [-1 0; 1 2], then the first variable has the range –1 to 1, and the second variable has the range 0 to 2 (each column corresponds to a variable).
Modify the value of the option InitialPopulationRange in the existing options, opts.
opts.InitialPopulationRange = [-1 0; 1 2];
Run the ga solver.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables,[],[],[], ...
[],[],[],[],opts);ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

fprintf('The number of generations is: %d\n', Output.generations);The number of generations is: 67
fprintf('The number of function evaluations is: %d\n', Output.funccount);The number of function evaluations is: 614
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -179.987
Reproduce Results
By default, ga starts with a random initial population created using MATLAB® random number generators. The solver produces the next generation using ga operators that also use these same random number generators. Every time a random number is generated, the state of the random number generators changes. So, even if you do not change any options, you can get different results when you run the solver again.
Run the solver twice to show this phenomenon.
Run the ga solver.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.484
Run ga again.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -185.867
ga gives different results in the two runs because the state of the random number generator changes from one run to another.
If you want to reproduce your results before you run ga, you can save the state of the random number stream.
thestate = rng;
Run ga.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.467
Reset the stream and rerun ga. The results are identical to the previous run.
rng(thestate); [x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.467
If you run ga before specifying to reproduce the results, you can reset the random number generator as long as you have the output structure.
strm = RandStream.getGlobalStream; strm.State = Output.rngstate.State;
Rerun ga. Again, the results are identical.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.467
Modify Stopping Criteria
ga uses four different criteria to determine when to stop the solver. ga stops when it reaches the maximum number of generations; by default, this number is 100 times the number of variables. ga also detects if the best fitness value does not change for some time given in seconds (stall time limit), or for some number of generations (maximum stall generations). Another criteria is the maximum time limit in seconds. Modify the stopping criteria to increase the maximum number of generations to 300 and the maximum stall generations to 100.
opts = optimoptions(opts,'MaxGenerations',300,'MaxStallGenerations', 100);
Rerun the ga solver.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables,[],[],[], ...
[],[],[],[],opts);ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

fprintf('The number of generations is: %d\n', Output.generations);The number of generations is: 299
fprintf('The number of function evaluations is: %d\n', Output.funccount);The number of function evaluations is: 2702
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.729
Specify ga Operators
ga starts with a random set of points in the population and uses operators to produce the next generation of the population. The different operators are scaling, selection, crossover, and mutation. The toolbox provides several functions to specify for each operator. Specify fitscalingprop for FitnessScalingFcn and selectiontournament for SelectionFcn.
opts = optimoptions(@ga,'SelectionFcn',@selectiontournament, ... 'FitnessScalingFcn',@fitscalingprop);
Rerun ga.
[x,Fval,exitFlag,Output] = ga(FitnessFunction,numberOfVariables,[],[],[], ...
[],[],[],[],opts);ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
fprintf('The number of generations is: %d\n', Output.generations);The number of generations is: 52
fprintf('The number of function evaluations is: %d\n', Output.funccount);The number of function evaluations is: 2497
fprintf('The best function value found is: %g\n', Fval);The best function value found is: -186.417
The best function value can improve or get worse based on the specified operators. Experimenting with different operators is often the best way to determine which set of operators works best for your problem.