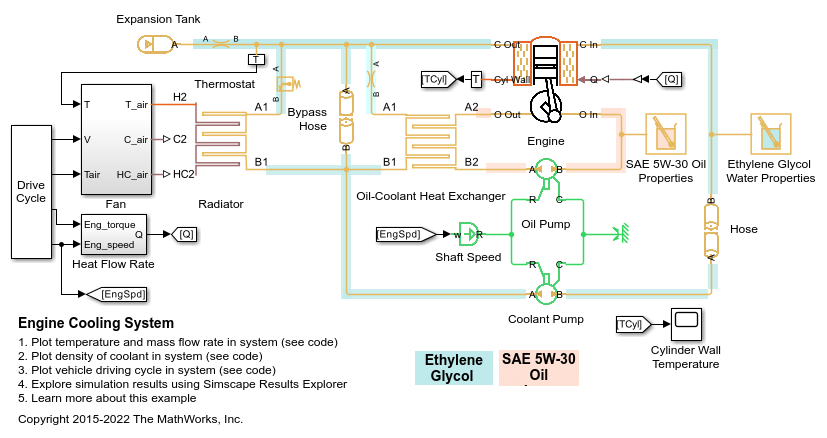
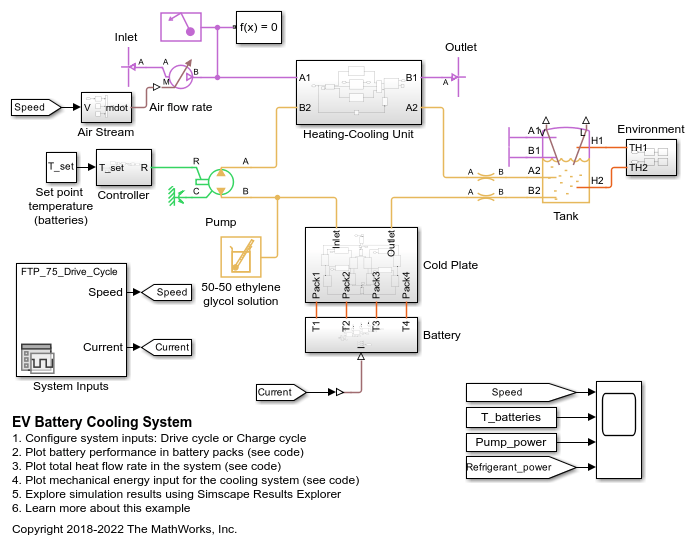
Thermal Liquid Properties (TL)
Preset fluid properties for the simulation of a thermal liquid network
Libraries:
Simscape /
Fluids /
Thermal Liquid /
Utilities
Description
The Thermal Liquid Properties (TL) block set predefined fluid properties to a thermal liquid network. The available fluids include pure water, aqueous mixtures, diesel, aviation fuel Jet A, and SAE 5W-30. You can use this block as a preset alternative to the Thermal Liquid Settings (TL) block. If your network does not have a connected liquid properties block, or the liquid defaults will apply. See Specify Fluid Properties for more details.
The preset fluid properties are defined in tabular form as functions of temperature and pressure. During simulation, the network properties are set by linear interpolation between data points. Tabular data for aqueous mixtures is provided for concentration by mass or volume.
All the fluid properties commonly specified in the Thermal Liquid Settings (TL) block are defined in the block. These properties include density, the bulk modulus and thermal expansion coefficient, the specific internal energy and specific heat, as well as the kinematic viscosity and thermal conductivity. The properties are valid over a limited region of temperatures and pressures specific to the fluid selected and dependent, in the cases of mixtures, on the concentration specified. Simulation is allowed within this validity region only.
Data Visualization
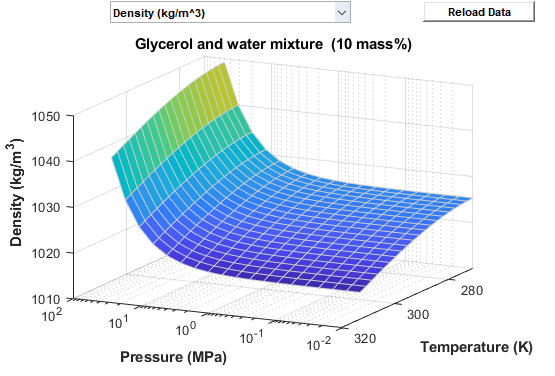
You can visualize the fluid properties defined in the block and the pressure and temperature regions of validity. To open the visualization utility, right-click the block and select Fluids > Plot Fluid Properties. The plot updates automatically upon selection of a fluid property from the drop-down list. Use the Reload Data button to regenerate the plot whenever the fluid selection or fluid parameters change.
Visualization of density data for a 10% glycerol aqueous mixture
Validity Regions
The validity regions are defined in the block as matrices of zeros and ones. Each row corresponds to a tabulated temperature and each column to a tabulated pressure. A zero denotes an invalid breakpoint and a one a valid breakpoint. These validity matrices are internal to the block and cannot be modified; they can only be checked (using the data visualization utility of the block).
In most cases, the validity matrices are extracted directly from the tabulated data. The glycol and glycerol mixtures pressure boundaries are not available from the data, and are obtained explicitly from block parameters. The figure below shows an example of the validity region for water. The shaded squares indicate temperature and pressure regions outside of the validity region.
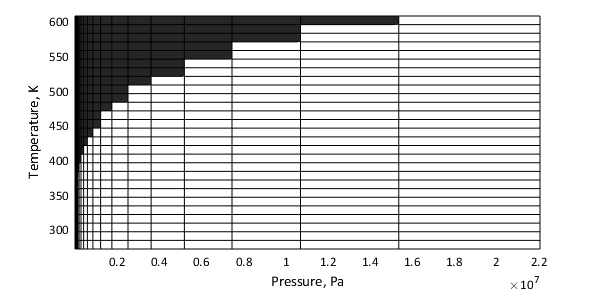
WaterThe properties of water are valid at temperatures above the triple-point value
(273.160 K) up to the critical-point value
(647.096 K). They are valid at pressures above the
greater of the triple-point value (611.657 Pa) on one hand
and the temperature-dependent saturation value on the other, up to the
critical-point value (22.064 MPa). Pressures below the
saturation point for a given temperature row are assigned a value of
0 in the validity matrix.
Seawater (MIT model)The properties of seawater are valid at temperatures above
0°C up to 120°C (273.15
K to 393.15 K); they are valid at pressures
above the saturation point up to a maximum value of 12 MPa.
Pressures below the saturation point for a given temperature row (and at the
specified concentration level) are assigned a value of 0 in
the validity matrix. Mixture concentrations can range in value from
0 to 0.12 on a mass fraction
basis.
Ethylene glycol and water mixtureThe properties of an aqueous ethylene glycol mixture are valid over a temperature domain determined from the mixture concentration; they are valid at pressures within the minimum and maximum bounds specified in the block dialog box (extended horizontally to span the width of the temperature rows).
The lower temperature bound is always the lesser of the minimum temperature
extracted from the available data and the freezing point of the mixture (the
mixture must be in the liquid state). The upper temperature bound is always the
maximum temperature extracted from the data. Mixture concentrations can range in
value from 0 to 0.6 if a mass-fraction
basis is used, or from 0 to 1 if a volume
fraction basis is used.
Propylene glycol and water mixtureThe properties of an aqueous propylene glycol mixture are valid over the
temperature and pressure ranges described for the case of Ethylene
glycol and water mixture. Mixture concentrations can range in
value from 0 to 0.6 if a mass-fraction
basis is used, or from 0.1 to 0.6 if a
volume fraction basis is used.
Glycerol and water mixtureThe properties of an aqueous glycerol mixture are valid over the temperature
and pressure ranges as described for the case of Ethylene glycol
and water mixture. Mixture concentrations can range in value
from 0 to 0.6 on a mass-fraction basis.
The properties are all extended to 100 degC as:
Density — quadratic fit
Alpha (density thermal derivative) — linear fit
Specific heat — linear fit
Specific internal energy — linear fit
Kinematic viscosity — exponential fit based on the upper half of the original temperature range
Dynamic viscosity — exponential fit based on the upper half of the original temperature range
Prandtl number — exponential fit based on the upper half of the original temperature range
Aviation fuel Jet-AThe properties of Jet A fuel are valid at temperatures above
-50.93°C up to 372.46°C
(222.22 K to 645.61 K); they are valid
at pressures above the saturation point up to a maximum value of 2.41
MPa. Pressures below the saturation point for a given temperature
row are assigned a value of 0 in the validity matrix.
Diesel fuelThe properties of diesel fuel are valid at temperatures above
-34.95°C up to 417.82°C
(238.20 K to 690.97 K); they are valid
at pressures above the saturation point up to a maximum value of 2.29
MPa. Pressures below the saturation point for a given temperature
row are assigned a value of 0 in the validity matrix.
SAE 5W-30The properties of SAE 5W-30 fuel derive from data that cover temperature and
pressure ranges for each property. The block uses measured properties between
29.85°C and 74.85°C (303
K to 348 K) and 7 MPa and
82 MPa. The block extrapolates data outside of this
region to -38°C and 200°C (235.15
K and 473.15 K) and to 0.01
MPa and 100 MPa. The way the block smooths and
extrapolates the data depends on the type of data:
Density — The block uses a quadratic fit. The block fits extrapolated regions to the bulk modulus and alpha fundamental relationships.
Bulk modulus — The block uses fundamental relationship with density based on the density quadratic fit. The block uses linear extrapolation in the extrapolation region.
Alpha (density thermal derivative) — The block uses the fundamental relationship with density based on density quadratic fit. The block uses linear extrapolation in the extrapolation region.
Specific heat — The block uses linear extrapolation in the extrapolation region. There is no dependency on pressure.
Thermal conductivity — The block uses linear extrapolation in the extrapolation region. There is no dependency on pressure.
Kinematic viscosity — The block uses the fundamental relationship with the fits of dynamic viscosity and density.
Dynamic viscosity — The block uses an exponential fit with temperature and a linear fit with pressure.
Prandtl number — The block uses the fundamental relationship with the fits of specific heat, dynamic viscosity, and thermal conductivity.
Calculated Properties
The density and thermal expansion coefficients of the aqueous mixtures of glycol and glycerol compounds are obtained from the block parameters. The fluid density, with respect to pressure and temperature, is calculated as:
where:
T is the network temperature.
p is the network pressure.
ρ is the fluid density.
pR is the reference pressure associated with the fluid property tables.
ß is the isothermal bulk modulus.
where the change in fluid density is evaluated as:
The thermal expansion coefficient is calculated as:
Examples
Ports
Conserving
Parameters
References
[1] Massachusetts Institute of Technology (MIT), Thermophysical properties of seawater database. http://web.mit.edu/seawater.
[2] K.G. Nayar, M.H. Sharqawy, L.D. Banchik, J.H. Lienhard V, Thermophysical properties of seawater: A review and new correlations that include pressure dependence, Desalination, Vol. 390, pp. 1-24, 2016.
[3] M.H. Sharqawy, J.H. Lienhard V, S.M. Zubair, Thermophysical properties of seawater: A review of existing correlations and data, Desalination and Water Treatment, Vol. 16, pp. 354-380.