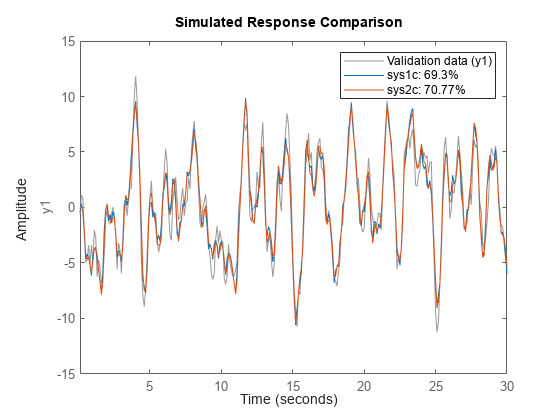
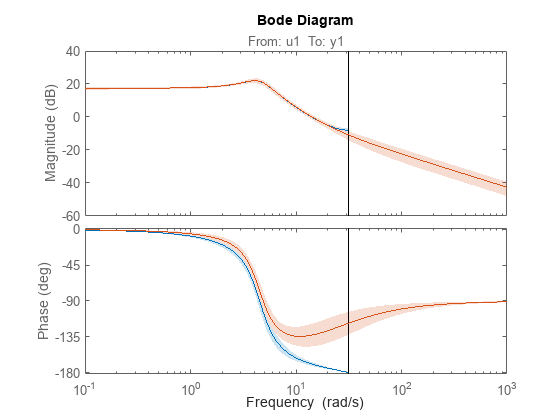
d2c
Convert model from discrete to continuous time
Description
sysc = d2c(sysd)sysd to a continuous-time model using zero-order hold on the
inputs.
Examples
Input Arguments
Output Arguments
References
[1] Franklin, G.F., Powell,D.J., and Workman, M.L., Digital Control of Dynamic Systems (3rd Edition), Prentice Hall, 1997.
[2] Kollár, I., G.F. Franklin, and R. Pintelon, "On the Equivalence of z-domain and s-domain Models in System Identification," Proceedings of the IEEE® Instrumentation and Measurement Technology Conference, Brussels, Belgium, June, 1996, Vol. 1, pp. 14-19.
Version History
Introduced before R2006a