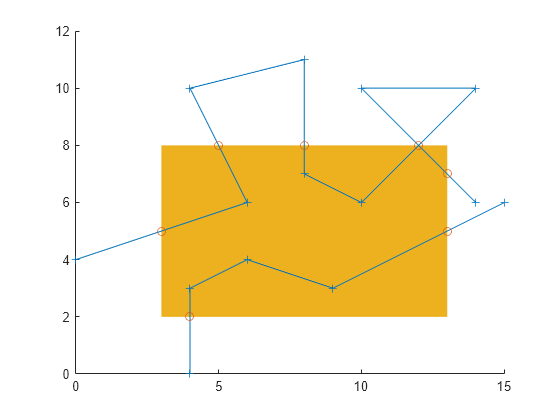
polyxpoly
Intersection points for lines or polygon edges
Description
[
returns the intersection points of two polylines in a planar, Cartesian system, with
vertices defined by xi,yi] = polyxpoly(x1,y1,x2,y2)x1, y1,
x2 and y2. The output arguments,
xi and yi, contain the
x- and y-coordinates of each point at
which a segment of the first polyline intersects a segment of the second. In the
case of overlapping, collinear segments, the intersection is actually a line segment
rather than a point, and both endpoints are included in xi,
yi.
[
returns a two-column array of line segment indices corresponding to the intersection
points. The k-th row of xi,yi,ii] = polyxpoly(___)ii indicates which
polyline segments give rise to the intersection point xi(k),
yi(k).
To remember how these indices work, just think of segments and vertices as fence
sections and posts. The i-th fence section connects the
i-th post to the (i+1)-th post. In
general, letting i and j denote the scalar
values comprised by the k-th row of ii, the
intersection indicated by that row occurs where the i-th segment
of the first polyline intersects the j-th segment of the second
polyline. But when an intersection falls precisely on a vertex of the first
polyline, then i is the index of that vertex. Likewise with the
second polyline and the index j. In the case of an intersection
at the i-th vertex of the first line, for example,
xi(k) equals x1(i) and
yi(k) equals y1(i). In the case of
intersections between vertices, i and j can be
interpreted as follows: the segment connecting x1(i),
y1(i) to x1(i+1),
y1(i+1) intersects the segment connecting
x2(j), y2(j) to
x2(j+1), y2(j+1) at the point
xi(k), yi(k).
Examples
Input Arguments
Output Arguments
Tips
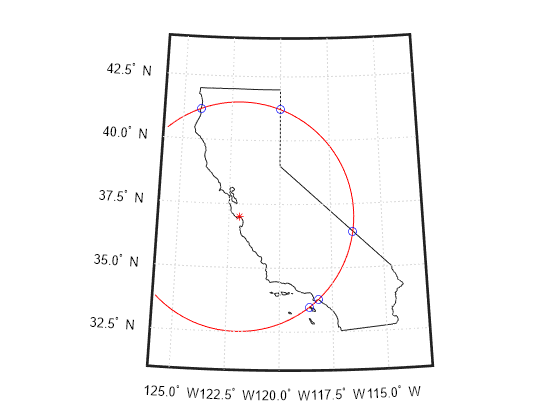
If the spacing between points is large, the intersections calculated by the
polyxpolyfunction and the intersections shown on a map display might be different. This is a result of differences between straight lines in the unprojected and projected coordinates. Similarly, there might be differences between thepolyxpolyresult and intersections that assume great circles or rhumb lines between points.
Version History
Introduced before R2006a